题目内容
【题目】已知![]() 中,D、E分别在AB、AC上,下列条件中,能推断
中,D、E分别在AB、AC上,下列条件中,能推断![]() 与
与![]() 相似的有( )个
相似的有( )个
①∠BDE+∠C=180°;②![]() ;③
;③![]() ;④∠A=90°,且
;④∠A=90°,且![]()
A.1B.2C.3D.4
【答案】C
【解析】
根据图形得到∠A是公共角,然后根据相似三角形的判定方法进行判断即可.
由图可知,
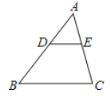
∠A是△ADE与△ACB的公共角,
①∵∠BDE+∠C=180°,∠ADE+∠BDE=180°,
∴∠ADE=∠C,
利用“两组角对应相等,两三角形相似”得到△ADE与△ACB相似;
②由ADAB=AEAC得到![]() ,可以利用“两边对应成比例,夹角相等,两三角形相似”得到△ADE与△ACB相似;
,可以利用“两边对应成比例,夹角相等,两三角形相似”得到△ADE与△ACB相似;
③由ADBC=ABDE可得到![]() ,公共角不是夹角,不能得到△ADE与△ACB相似;
,公共角不是夹角,不能得到△ADE与△ACB相似;
④∵![]() ,∠A=90°,
,∠A=90°,
利用“斜边和一条直角边对应成比例的两个直角三角形相似”得到△ADE与△ACB相似,
综上所述,能判断△ADE与△ACB相似的是①②④,共3个.
故选:C.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目