题目内容
【题目】在平面直角坐标系xOy中,抛物线![]() 与直线
与直线![]() 交于A, B两点,其中点A在x轴上.
交于A, B两点,其中点A在x轴上.
(1)用含有b的代数式表示c;
(2)① 若点B在第一象限,且![]() ,求抛物线的解析式;
,求抛物线的解析式;
② 若![]() ,结合函数图象,直接写出b的取值范围.
,结合函数图象,直接写出b的取值范围.
【答案】(1)c=b-1;
(2)①抛物线的解析式为![]() ;②
;② ![]() 或
或![]() .
.
【解析】
(1)由题意直线y=x+1与x轴交于点A,可得出点A坐标 ,又因抛物线y=x2+bx+c经过点A,所以将点A坐标代入抛物线解析式可解得.
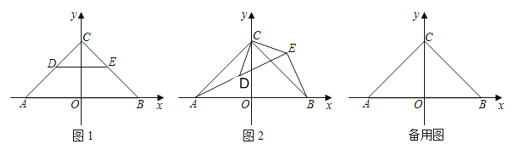
(2)①由y=x+1可推得∠OAC=45.
如图,已知AB=3![]() ,
, 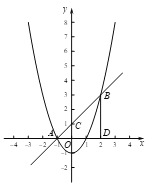
Rt△ABD中,利用勾股定理可解出AD=BD=3,所以点B的坐标为(2,3) .
将点B的坐标(2,3)代入抛物线y=x2+bx+c的解析式可得2b+c=-1.
并与(1)中得到的c=b-1联立方程组并解出方程组可得b,c的值,带入得到
抛物线的解析式.
②因为![]() ,结合函数图象,可直接得出b的取值范围.
,结合函数图象,可直接得出b的取值范围.![]() 或
或![]() .
.
解:(1)由题意直线y=x+1与x轴交于点A
可得点A坐标为(-1,0)
又因抛物线y=x2+bx+c经过点A
所以将点A坐标(-1,0)代入抛物线解析式可得
1-b+c=0,即c=b-1.
(2)①设y=x+1与y轴交于点C,可得
A (-1,0),C (0,1).
可知OA=OC=1.
又因∠AOC=90,
所以∠OAC=45.
如图,已知AB=3![]() ,过B作BD⊥x轴于点D,
,过B作BD⊥x轴于点D,

易知∠ADB=90.
又因∠BAD=45,AB=3![]() ,
,
所以AD=BD=3.
所以点B的坐标为(2,3) .
将点B的坐标(2,3)代入抛物线y=x2+bx+c的解析式可得2b+c=-1.
并与(1)中得到的c=b-1联立方程组可得:
![]() 解得
解得![]()
得抛物线的解析式为![]() .
.
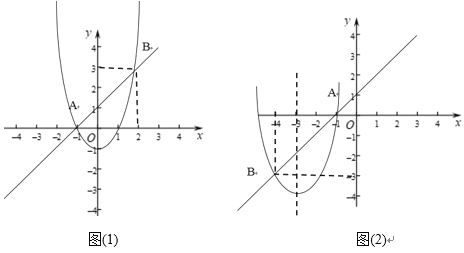
②因为![]() ,由函数图象(1)得, 对称轴
,由函数图象(1)得, 对称轴![]() 即b≤0.
即b≤0.
由函数图象(2)得, 对称轴![]() 即b≥6.
即b≥6.
所以可得出b的取值范围![]() 或
或![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案