题目内容
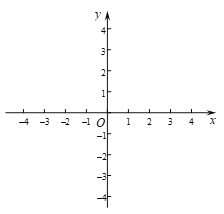
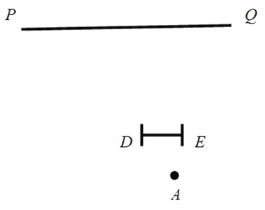
【题目】如图1,在平面直角坐标系中,点A(﹣![]() ,0),B(
,0),B(![]() ,0),C(0,
,0),C(0,![]() ).D,E分别是线段AC和CB上的点,CD=CE.将△CDE绕点C逆时针旋转一个角度α.
).D,E分别是线段AC和CB上的点,CD=CE.将△CDE绕点C逆时针旋转一个角度α.
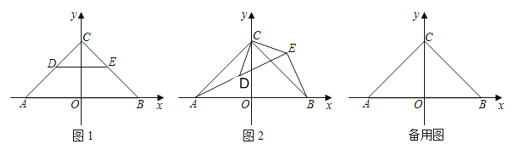
(1)若0°<α<90°,在旋转过程中当点A,D,E在同一直线上时,连接AD,BE,如图2.求证:AD=BE,且AD⊥BE
(2)若0°<α<360°,D,E恰好是线段AC和CB上的中点,在旋转过程中,当DE∥AC时,求α的值及点E的坐标.
【答案】(1)证明见解析;(2)α=45°时,点E的坐标为(1,![]() );α=225°时,点E的坐标为(﹣1,
);α=225°时,点E的坐标为(﹣1,![]() )
)
【解析】
(1)证明△ACD≌△BCE,可得AD=BE,∠CAD=∠CBE,则结论得证;
(2)由勾股定理求出AC长,可求出CD 的长,如图1,当α=∠ACO=45°时,求出点E的坐标为(1,![]() ),如图2,当α=∠ACD=180°+∠ACO=225°时,求出点E的坐标为(﹣1,
),如图2,当α=∠ACD=180°+∠ACO=225°时,求出点E的坐标为(﹣1,![]() ).
).
(1)∵点A(﹣![]() ,0),B(
,0),B(![]() ,0),C(0,
,0),C(0,![]() ),
),
∴OC垂直平分AB,OA=OB=OC,
∴AC=BC,∠CAB=∠CBA=45°,∠ACB=90°,
根据旋转的性质得,∠ACD=∠BCE,
又∵AC=BC,CD=CE,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠CAD=∠CBE,
∴∠BAE+∠ABE=(∠CAB﹣∠CAD)+(∠ABC+∠CBE)=90°,
∴∠AEB=180°﹣(∠BAE+∠ABE)=90°,即AD⊥BE;
(2)由(1)知,∠ACB=90°,AC=BC,
在Rt△AOC中,AC=![]() =2,
=2,
∵D,E是线段AC和CB上的中点,
∴![]() =1,
=1,
如图1,当α=∠ACO=45°时,即∠ACO=∠CDE=45°,
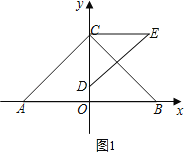
∴AC∥DE,
此时点E的坐标为(1,![]() ),
),
如图2,当α=∠ACD=180°+∠ACO=225°时,
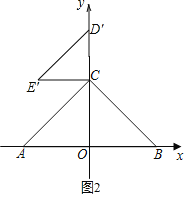
即∠ACO=∠CD′E′=45°,
∴AC∥D′E′,
此时点E的坐标为(﹣1,![]() ).
).