Question

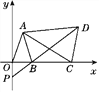
【题目】如图，在平面直角坐标系中，抛物线y=x2经过平移得到抛物线y=x2﹣2x ， 其对称轴与两抛物线所围成的阴影部分的面积是 ．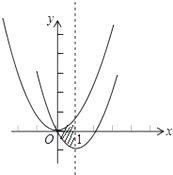

Answer 1

【答案】1
【解析】先利用配方法得到抛物线y=x2-2x的顶点坐标为（1，-1），则抛物线y=x2向右平移1个单位，向下平移1个单位得到抛物线y=x2-2x，然后利用阴影部分的面积等于三角形面积进行计算． 解：y=x2-2x=（x-1）2-1，即平移后抛物线的顶点坐标为（1，-1）， 所以抛物线y=x2向右平移1个单位，向下平移1个单位得到抛物线y=x2-2x， 所以对称轴与两抛物线所围成的阴影部分的面积= ×1×2=1． 故答案为1．

根据已知可知两图像是通过平移得到的，因此它们的形状和大小一样，先求出平移后的顶点坐标，及对称轴，要求其对称轴与两抛物线所围成的阴影部分的面积转化为求三角形的面积，即可求出结果。