题目内容
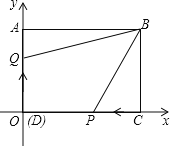
【题目】如图,抛物线y=ax2+bx+c的开口向下,与x轴和y轴分别交于点A(﹣4,0)和点B(0,2),过点B作BC⊥AB交抛物线于点C,连接AC,且∠BAC=∠BAO. 
(1)求BC的长;
(2)求抛物线的解析式.
【答案】
(1)解:在Rt△AOB中,由勾股定理,得
AB= ![]() =2
=2 ![]() .
.
∵BC⊥AB,
∴∠ABC=∠AOB=90°,
∵∠CAB=∠BAO,
∴△CAB∽△BAO,
![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
BC= ![]()
(2)解:设C点坐标为(m,n),由勾股定理,
AC= ![]() =5.
=5.
AC2=25,BC2=5,
即  ,
,
解得m=﹣1,m=1(舍),n=4,
即C点坐标(﹣1,4).
将A,B,C点坐标代入函数解析式,得
 ,
,
解得  ,
,
抛物线的解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+2
x+2
【解析】(1)根据勾股定理,可得AB的长,根据相似三角形的判定与性质,可得答案;(2)根据两点间的距离,可得两个方程,根据解方程,可得C点坐标,根据待定系数法,可得函数解析式.
【考点精析】根据题目的已知条件,利用抛物线与坐标轴的交点和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目