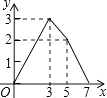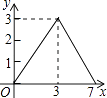��Ŀ����
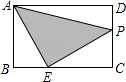
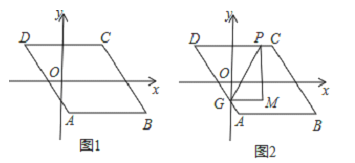
����Ŀ����ͼ1����֪��ABCD��AB��x�ᣬAB=6����A������Ϊ��1����4������D������Ϊ����3��4������B�ڵ������ޣ���P����ABCD���ϵ�һ�����㣮
��1������P�ڱ�BC�ϣ�PD=CD�����P�����꣮
��2������P�ڱ�AB��AD�ϣ���P����������ԳƵĵ�Q����ֱ��y=x��1�ϣ����P�����꣮
��3������P�ڱ�AB��AD��CD�ϣ���G��AD��y��Ľ��㣬��ͼ2������P��y���ƽ����PM������G��x���ƽ����GM�������ཻ�ڵ�M������PGM��ֱ��PG���ۣ�����M�Ķ�Ӧ��������������ʱ�����P�����꣮��ֱ��д������
���𰸡���1����P����Ϊ��3��4������2����P������Ϊ����3��4����1��0����5����4����3����4������3����P����Ϊ��2����4����![]() ��3����
��3����![]() ��4����
��4����![]() ��4����
��4����
�������������������1����P��BC�ϣ�ҪʹPD=CD��ֻ��P��C�غϣ�
��2������Ҫ�ֵ�P�ڱ�AB��AD��ʱ���ۣ���������P����������ԳƵĵ�Q��������Ҫϸ������P����x��ĶԳƵ�Q�͵�P����y��ĶԳƵ�Q�����ۣ����ݹ���x�ᡢy��ԳƵ������������x��Գ�ʱ����ĺ����겻�䣬���������෴��������y��Գ�ʱ���෴�������õ��ĵ�Q���������ֱ��y=x-1�����ɽ��
��3���ڲ�ͬ���ϣ�����ͼ��M���ۺ�M������x�ỹ��y�ᣬ������������⣮
�����������1����CD=6������P���C�غϣ�����P�������ǣ�3��4����
��2��������P�ڱ�AD��ʱ������֪�ã�ֱ��AD�ĺ�������ʽΪ��![]() ����P��a��-2a-2������-3��a��1��
����P��a��-2a-2������-3��a��1��
����P����x��ԳƵ�Q1��a��2a+2����ֱ��y=x-1�ϣ���2a+2=a-1�����a=-3����ʱP��-3��4����
����P����y��ԳƵ�Q2��-a��-2a-2����ֱ��y=x-1�ϣ���-2a-2=-a-1�����a=-1����ʱP��-1��0����
������P�ڱ�AB��ʱ����P��a��-4������1��a��7��
����P����x��ԳƵ�Q3��a��4����ֱ��y=x-1�ϣ���4=a-1�����a=5����ʱP��5��-4����
����P����y��ԳƵ�Q4��-a��-4����ֱ��y=x-1�ϣ���-4=-a-1�����a=3����ʱP��3��-4����
������������P��������-3��4����-1��0����5��-4����3��-4����
��3����Ϊֱ��ADΪy=-2x-2������G��0��-2����
����ͼ������P��CD����ʱ������P��m��4������-3��m��3����ɵ�M��P=PM=4+2=6��M��G=GM=|m|����֤����OGM��ס�HM��P����![]() ����
����![]() ����OM��=
����OM��=![]() ����Rt��OGM���У��ɹ��ɶ����ã�
����Rt��OGM���У��ɹ��ɶ����ã�![]() �����m=-
�����m=-![]() ��
��![]() ����P��-
����P��-![]() ��4����
��4����![]() ��4����
��4����
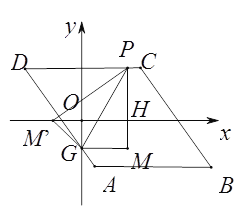
������ͼ������P��AD����ʱ����P��m��-2m-2������PM��=PM=|-2m|��GM��=MG=|m|����֤����OGM��ס�HM��P����![]() ����
����![]() ����OM��=
����OM��=![]() ����Rt��OGM���У��ɹ��ɶ����ã�
����Rt��OGM���У��ɹ��ɶ����ã�![]() ��������m= -
��������m= -![]() ����P��-
����P��-![]() ��3����
��3����
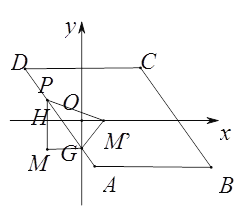
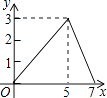
����ͼ������P��AB����ʱ����P��m��-4������ʱM����y���ϣ����ı���PM��GM�������Σ�����GM=PM=4-2=2����P��2��-4����
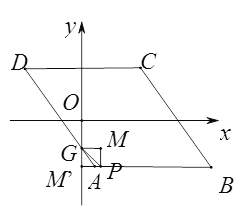
������������P��������2��-4����-![]() ��3����-
��3����-![]() ��4����
��4����![]() ��4����
��4����

����Ŀ��ijУΪ�˽���꼶ѧ����������������꼶��ѧ��������һ���������飬�����������ݽ���ͳ�����������Ƴ�����Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��һ���֣�
���� | Ƶ�����ˣ� | Ƶ�� |
4.0��x��4.3 | 20 | 0.1 |
4.3��x��4.6 | 40 | 0.2 |
4.6��x��4.9 | 70 | 0.35 |
4.9��x��5.2 | a | 0.3 |
5.2��x��5.5 | 10 | b |
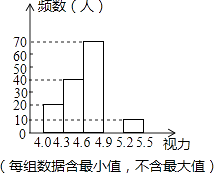
��1����Ƶ���ֲ����У�a= �� b=��
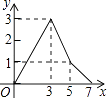
��2����Ƶ���ֲ�ֱ��ͼ����������
��3����������4.6���ϣ���4.6����������������������������ռ�����������İٷֱ��Ƕ��٣�