题目内容
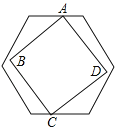
【题目】如图，有一个边长不定的正方形ABCD，它的两个相对的顶点A，C分别在边长为1的正六边形一组平行的对边上，另外两个顶点B，D在正六边形内部（包括边界），则正方形边长a的取值范围是 ．
【答案】
≤a≤
．
【解析】
试题分析：①当正方形ABCD的对角线AC在正六边形一组平行的对边的中点上时，正方形边长a的值最小，AC是正方形的对角线，∴AC=A′D=
，∴a=；
②当正方形ABCD的四个顶点都在正六边形的边上时，正方形边长a的值最大，AC是正方形的对角线AC，则△AEB是等腰三角形，四边形AFGD是等腰梯形，过F，G分别作FH⊥AD，GN⊥AD，设AE=x，则AF=1﹣x，∴AB=x，AH=DN=
（1﹣x），∴AD=1+（1﹣x），∴x=1+（1﹣x），∴x=
，∴AB=，∴正方形边长a的取值范围是：≤a≤，故答案为：≤a≤．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
