Question

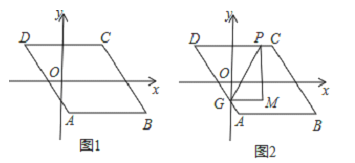
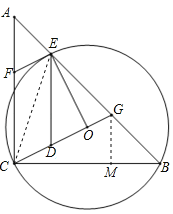
【题目】（本题10分）如图，在△ABC中，AC=BC，∠ACB=90°，⊙O（圆心O在△ABC内部）经过B、C两点，交AB于点E，过点E作⊙O的切线交AC于点F．延长CO交AB于点G，作ED∥AC交CG于点D

（1）求证：四边形CDEF是平行四边形；

（2）若BC=3，tan∠DEF=2，求BG的值．

Answer 1

【答案】(1)证明见解析；（2）．

【解析】

试题分析：（1）连接CE，根据等腰直角三角形的性质得到∠B=45°，根据切线的性质得到∠FEC=∠B=45°，∠FEO=90°，根据平行线的性质得到∠ECD=∠FEC=45°，得到∠EOC=90°，求得EF∥OD，于是得到结论；

（2）过G作GN⊥BC于N，得到△GMB是等腰直角三角形，得到MB=GM，根据平行四边形的性质得到∠FCD=∠FED，根据余角的性质得到∠CGM=∠ACD，等量代换得到∠CGM=∠DEF，根据三角函数的定义得到CM=2GM，于是得到结论．

试题解析：（1）连接CE，

∵在△ABC中，AC=BC，∠ACB=90°，

∴∠B=45°，

∵EF是⊙O的切线，

∴∠FEC=∠B=45°，∠FEO=90°，

∴∠CEO=45°，

∵DE∥CF，

∴∠ECD=∠FEC=45°，

∴∠EOC=90°，

∴EF∥OD，

∴四边形CDEF是平行四边形；

（2）过G作GN⊥BC于N，

∴△GMB是等腰直角三角形，

∴MB=GM，

∵四边形CDEF是平行四边形，

∴∠FCD=∠FED，

∵∠ACD+∠GCB=∠GCB+∠CGM=90°，

∴∠CGM=∠ACD，

∴∠CGM=∠DEF，

∵tan∠DEF=2，

∴tan∠CGM==2，

∴CM=2GM，

∴CM+BM=2GM+GM=3，

∴GM=1，

∴BG=GM=．