题目内容
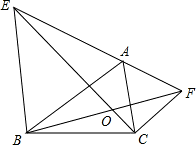 如图,△ABE和△ACF分别是以△ABC的AB、AC为边的正三角形,CE、BF相交于O.则∠EOB的度数为
如图,△ABE和△ACF分别是以△ABC的AB、AC为边的正三角形,CE、BF相交于O.则∠EOB的度数为
- A.45°
- B.60°
- C.70°
- D.90°
B
分析:首先根据题意推出△AEC≌△ABF,根据∠AEO+∠BEO=60°,推出∠BEO+∠ABO=60°,即得∠BEO+∠ABO+∠EBA=120°,根据三角形内角和定理,即可推出∠EOB=60°.
解答:∵∠EAB=∠FAC,
∴∠EAC=∠BAF,
在△AEC和△ABF中,
∵AE=AB,∠EAC=∠BAF,AC=AF,
∴△AEC≌△ABF,
∴∠AEO=∠ABO
∵∠AEO+∠BEO=60°
∴∠BEO+∠ABO=60°
∵在△EBO中,∠BEO+∠ABO=60°,∠EBA=60°,∠BEO+∠ABO+∠EBA=120°
∴∠EOB=60°
故选择B.
点评:本题主要考查全等三角形的判定和性质、三角形内角和定理,关键在于通过求证△AEC≌△ABF,推出∠BEO+∠ABO+∠EBA=120°.
分析:首先根据题意推出△AEC≌△ABF,根据∠AEO+∠BEO=60°,推出∠BEO+∠ABO=60°,即得∠BEO+∠ABO+∠EBA=120°,根据三角形内角和定理,即可推出∠EOB=60°.
解答:∵∠EAB=∠FAC,
∴∠EAC=∠BAF,
在△AEC和△ABF中,
∵AE=AB,∠EAC=∠BAF,AC=AF,

∴△AEC≌△ABF,
∴∠AEO=∠ABO
∵∠AEO+∠BEO=60°
∴∠BEO+∠ABO=60°
∵在△EBO中,∠BEO+∠ABO=60°,∠EBA=60°,∠BEO+∠ABO+∠EBA=120°
∴∠EOB=60°
故选择B.
点评:本题主要考查全等三角形的判定和性质、三角形内角和定理,关键在于通过求证△AEC≌△ABF,推出∠BEO+∠ABO+∠EBA=120°.

练习册系列答案
相关题目
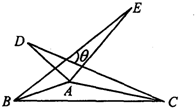 17、如图,△ABE和△ACD是△ABC分别沿着AB,AC边翻折180°形成的,若∠BAC=150°,则∠θ的度数是
17、如图,△ABE和△ACD是△ABC分别沿着AB,AC边翻折180°形成的,若∠BAC=150°,则∠θ的度数是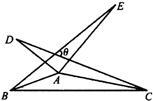 5、如图,△ABE和△ACD是△ABC分别沿着AB,AC边翻折180°形成的,若∠BAC=150°,则∠θ的度数是( )
5、如图,△ABE和△ACD是△ABC分别沿着AB,AC边翻折180°形成的,若∠BAC=150°,则∠θ的度数是( )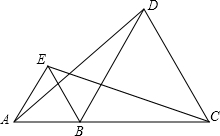
 如图,△ABE和△ACD中,给出以下四个论断:
如图,△ABE和△ACD中,给出以下四个论断: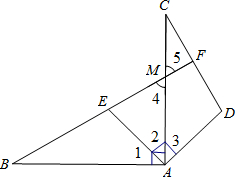 如图,△ABE和△ACD有公共点A,∠BAC=∠DAE=90°,AB=AC,AE=AD,延长BE分别交AC、CD于点M、F.求证:
如图,△ABE和△ACD有公共点A,∠BAC=∠DAE=90°,AB=AC,AE=AD,延长BE分别交AC、CD于点M、F.求证: