题目内容
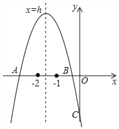
【题目】抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于C点,其中﹣2<h<﹣1,﹣1<xB<0,下列结论①abc<0;②(4a﹣b)(2a+b)<0;③4a﹣c<0;④若OC=OB,则(a+1)(c+1)>0,正确的为( )
A. ①②③④ B. ①②④ C. ①③④ D. ①②③
【答案】C
【解析】分析:①由抛物线对称轴位置确定ab的符号,由抛物线与y轴的交点判断c与0的关系,进而对所得结论进行判断;
②根据对称轴公式和-2<h<-1可得:4a-b<0,根据a<0,b<0可知:2a+b<0,可作判断;
③根据b>4a,得2b-8a>0①,当x=-2时,4a-2b+c>0②,两式相加可得结论;
④根据OB=OC可知:c是方程ax2+bx+c=0的一个根,代入后可得:ac+b+1=0,则ac=-b-c,将所求的式子去括号再将ac的式子代入可得结论.
详解:①∵抛物线开口向下,
抛物线对称轴位于y轴的左侧,则a、b同号,故ab>0,
抛物线与y轴交于负半轴,则c<0,故abc<0,
故①正确;
②∵抛物线开口方向向下,
∴a<0,
∵x=-![]() =h,且-2<h<-1,
=h,且-2<h<-1,
∴4a<b<2a,
∴4a-b<0,
又∵h<0,
∴-![]() <1
<1
∴2a+b<0,
∴(4a-b)(2a+b)>0,
故②错误;
③由②知:b>4a,
∴2b-8a>0①.
当x=-2时,4a-2b+c>0②,
由①+②得:4a-8a+c>0,即4a-c<0.
故③正确;
④∵当x=-1时,a-b+c>0,
∵OC=OB,
∴当x=c时,y=0,即ac2+bc+c=0,
∵c≠0,
∴ac+b+1=0,
∴ac=-b-1,
则(a+1)(c+1)=ac+a+c+1=-b-1+a+c+1=a-b+c>0,
故④正确;
所以本题正确的有:①③④,
故选C.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案【题目】![]() 年
年![]() 月
月![]() 日是第
日是第![]() 个世界读书日,为迎接第
个世界读书日,为迎接第![]() 个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座.大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;
个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座.大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;
参赛者 | 推荐语 | 读书心得 | 读书讲座 |
甲 |
|
|
|
乙 |
|
|
|
(1)若将三项成绩的平均分作为参赛选手的综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
(2)若“推荐语”“读书心得”“读书讲座”的成绩按![]() 确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.