题目内容
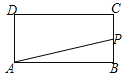
【题目】如图,在△ABD中,AB=AD, 将△ABD沿BD翻折,使点A翻折到点C. E是BD上一点,且BE>DE,连结CE并延长交AD于F,连结AE.
(1)依题意补全图形;
(2)判断∠DFC与∠BAE的大小关系并加以证明;
(3)若∠BAD=120°,AB=2,取AD的中点G,连结EG,求EA+EG的最小值.


【答案】(1)见解析;(2)判断:∠DFC=∠BAE. 证明见解析;(3)EA+EG的最小值为![]() .
.
【解析】(1)将△ABD沿BD翻折,使点A翻折到点C.E是BD上一点,且BE>DE,连结CE并延长交AD于F,连结AE,据此画图即可;(2)根据△ABE≌△CBE(SAS),可得∠BAE=∠BCE.再根据AD∥BC,可得∠DFC=∠BCE,进而得出∠DFC=∠BAE;(3)连接CG,AC,根据EC+EG≥CG可知,CG长就是EA+EG的最小值,根据△ACD为边长为2的等边三角形,G为AD的中点,运用勾股定理即可得出CG=![]() ,进而得到EA+EG的最小值.
,进而得到EA+EG的最小值.
(1)补全图形如下:
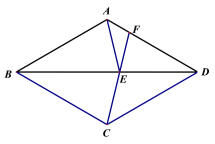
(2)判断:∠DFC=∠BAE.
证明:∵将△ABD沿BD翻折,使点A翻折到点C.
∴BC=BA=DA=CD. ∴四边形ABCD为菱形.
∴∠ABD=∠CBD,AD∥BC.
又∵BE=BE,∴△ABE≌△CBE(SAS).
∴∠BAE=∠BCE.
∵AD∥BC,
∴∠DFC=∠BCE.
∴∠DFC=∠BAE.
(3)连CG, AC.
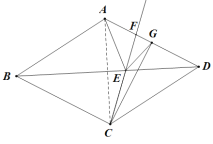
由![]() 轴对称可知,EA+EG=EC+EG,
轴对称可知,EA+EG=EC+EG,
CG长就是EA+EG的最小值.
∵∠BAD=120°,四边形ABCD为菱形,
∴∠CAD=60°.
∴△ACD为边长为2的等边三角形.
可求得CG=![]() .
.
∴EA+EG的最小值为![]() .
.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目