��Ŀ����
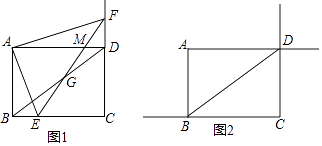
����Ŀ����ͼ����֪��ABD�͡�CEF����б��Ϊ2cm��ȫ��ֱ�������Σ����С�ABD=��FEC=60�㣬��B��D��C��E����ͬһֱ���ϣ�DC=4��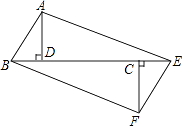
��1����֤���ı���ABFE��ƽ���ı��Σ�
��2����ABD����BE�ķ�����ÿ��1cm���ٶ��˶������ABD�˶���ʱ��Ϊt�룬
�ٵ�tΪ��ֵʱ��ABFE�����Σ���˵��������ɣ�
��ABFE�п����Ǿ����������ܣ����t��ֵ���˾��ε�������������ܣ���˵�����ɣ�
���𰸡�
��1��
֤��������֪��ABD�͡�CEF����б��Ϊ2cm��ȫ��ֱ�������Σ�
��AB=EF��
�ߡ�ABD=��FEC��
��AB��EF����AB=EF��
���ı���ABFE��ƽ���ı���
��2��
�ٵ�t=4ʱ��ABFE�����Σ�
�������£��ߡ�ABD����BE�ķ�����ÿ��1cm���ٶ��˶���
4���ABD�ƶ��ľ���Ϊ4��1=4����DC=4��
��D��C�غϣ�
��AF��BE�����ı���ABFE��ƽ���ı��Σ�
���ı���ABFE�����Σ�
�ڵ��ı���ABFE�Ǿ���ʱ����BAE=90�㣬
�ߡ�ABD=60�㣬
���BEA=30�㣬
��BE=2AB=4��AE= ![]() =2
=2 ![]() ��
��
�ߡ�ABD=60�㣬AB=2��
��BD=1��ͬ��CE=1��
��CD=4��1��1=2��
t=2��1=2�룬���ε����=AB��AE=4 ![]() cm2
cm2
����������1������ȫ�������ε����ʵõ�AB=EF������ƽ���ߵ��ж�����֤��AB��EF������ƽ���ı��ε��ж�����֤�����ۣ���2���ٸ��ݡ�ABD���ƶ��ٶȺ�ʱ��õ�D��C�غϣ��������ε��ж�������ɣ��ڸ��ݾ��ε����ʺ����ҵĶ������BE���������еĶ������AE�����CD�ij����õ�t��ֵ�����ݾ��ε������ʽ��������
�����㾫��������ƽ���ı��ε��ж��������ǽ����ĸ�������Ҫ֪����һֱ�߹�ƽ���ı������Խ��ߵĽ��㣬������ֱ�߱�һ��Ա߽��µ��߶��ԶԽ��ߵĽ���Ϊ�е㣬����������ֱ�߶��ȷִ�ƽ���ı��ε������

 �ƸԹھ��ο���ϵ�д�
�ƸԹھ��ο���ϵ�д�����Ŀ��Ϊ�˱���������ij�������ۺ�����ָ�Ӳ���������A��B�����ͺŵ���ˮ�����豸��10̨����֪��90��Ԫ����A�ͺŵ���ˮ�����豸��̨������75��Ԫ����B�ͺŵ���ˮ�����豸��̨����ͬ��ÿ̨�豸�۸��´�����ˮ�����±���ʾ��
��ˮ�����豸 | A�� | B�� |
�۸���Ԫ/̨�� | m | m��3 |
�´�����ˮ������/̨�� | 220 | 180 |
��1����m��ֵ��
��2���������ʽ����ƣ�ָ�Ӳ����ڹ�����ˮ�����豸���ʽ���165��Ԫ�����ж����ֹ����������ÿ����ദ����ˮ���Ķ�����