ƒøƒ⁄»ð
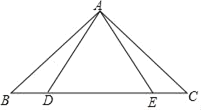
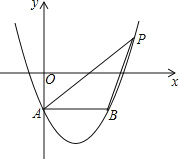
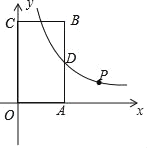
°æƒø°ø»ÁÕº£¨æÿ–ŒOABCµƒ∂•µ„A‘⁄x÷·’˝∞Î÷·…œ£¨∂•µ„C‘⁄y÷·’˝∞Î÷·…œ£¨µ„Bµƒ◊¯±ÍŒ™£®4£¨m£©£®5°Ðm°Ð7£©£¨∑¥±»¿˝∫Ø ˝y£Ω![]() £®x£æ0£©µƒÕºœÛΩª±þAB”⁄µ„D£Æ
£®x£æ0£©µƒÕºœÛΩª±þAB”⁄µ„D£Æ
£®1£©”√mµƒ¥˙ ˝ Ω±Ì æBDµƒ≥§£ª
£®2£©…˵„P‘⁄∏√∫Ø ˝ÕºœÛ…œ£¨«“À¸µƒ∫·◊¯±ÍŒ™m£¨¡¨Ω·PB£¨PD
¢Ÿº«æÿ–ŒOABC√ʪ˝”ΰ˜PBD√ʪ˝÷Æ≤ÓŒ™S£¨«Ûµ±mŒ™∫Œ÷µ ±£¨S»°µΩ◊Ó¥Û÷µ£ª
¢⁄Ω´µ„D»∆µ„PƒÊ ±’Ζ˝◊™90°„µ√µΩµ„E£¨µ±µ„E«°∫√¬‰‘⁄x÷·…œ ±£¨«Ûmµƒ÷µ£Æ
°æ¥∞∏°ø£®1£©BD£Ωm©Å4£®2£©¢Ÿm£Ω7 ±£¨S»°µΩ◊Ó¥Û÷µ¢⁄m£Ω2+2![]()
°æΩ‚Œˆ°ø
£®1£©œ»»∑∂®≥ˆµ„D∫·◊¯±ÍŒ™4£¨¥˙»Î∑¥±»¿˝∫Ø ˝Ω‚Œˆ Ω÷–«Û≥ˆµ„D∫·◊¯±Í£¨º¥ø…µ√≥ˆΩ·¬€£ª
£®2£©¢Ÿœ»«Û≥ˆæÿ–ŒOABCµƒ√ʪ˝∫Õ»˝Ω«–ŒPBDµƒ√ʪ˝µ√≥ˆS£Ω©Å![]() £®m©Å8£©2+24£¨º¥ø…µ√≥ˆΩ·¬€£ª¢⁄¿˚”√“ªœþ»˝÷±Ω«≈–∂œ≥ˆDG£ΩPF£¨Ω¯∂¯«Û≥ˆµ„Pµƒ◊¯±Í£¨º¥ø…µ√≥ˆΩ·¬€£Æ
£®m©Å8£©2+24£¨º¥ø…µ√≥ˆΩ·¬€£ª¢⁄¿˚”√“ªœþ»˝÷±Ω«≈–∂œ≥ˆDG£ΩPF£¨Ω¯∂¯«Û≥ˆµ„Pµƒ◊¯±Í£¨º¥ø…µ√≥ˆΩ·¬€£Æ
Ω‚£∫£®1£©°þÀƒ±þ–ŒOABC «æÿ–Œ£¨
°ýAB°Õx÷·…œ£¨
°þµ„B£®4£¨m£©£¨
°ýµ„Dµƒ∫·◊¯±ÍŒ™4£¨
°þµ„D‘⁄∑¥±»¿˝∫Ø ˝y£Ω![]() …œ£¨
…œ£¨
°ýD£®4£¨4£©£¨
°ýBD£Ωm©Å4£ª
£®2£©¢Ÿ»ÁÕº1£¨°þæÿ–ŒOABCµƒ∂•µ„Bµƒ◊¯±ÍŒ™£®4£¨m£©£¨
°ýSæÿ–ŒOABC£Ω4m£¨
”…£®1£©÷™£¨D£®4£¨4£©£¨
°ýS°˜PBD£Ω![]() £®m©Å4£©£®m©Å4£©£Ω
£®m©Å4£©£®m©Å4£©£Ω![]() £®m©Å4£©2£¨
£®m©Å4£©2£¨
°ýS£ΩSæÿ–ŒOABC©ÅS°˜PBD£Ω4m©Å![]() £®m©Å4£©2£Ω©Å
£®m©Å4£©2£Ω©Å![]() £®m©Å8£©2+24£¨
£®m©Å8£©2+24£¨
°ý≈◊ŒÔœþµƒ∂‘≥∆÷·Œ™m£Ω8£¨
°þa£º0£¨5°Ðm°Ð7£¨
°ým£Ω7 ±£¨S»°µΩ◊Ó¥Û÷µ£ª
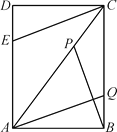
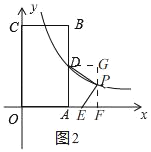
¢⁄»ÁÕº2£¨π˝µ„P◊˜PF°Õx÷·”⁄F£¨π˝µ„D◊˜DG°ÕFPΩªFPµƒ—”≥§œþ”⁄G£¨
°ý°œDGP£Ω°œPFE£Ω90°„£¨
°ý°œDPG+°œPDG£Ω90°„£¨
”…–˝◊™÷™£¨PD£ΩPE£¨°œDPE£Ω90°„£¨
°ý°œDPG+°œEPF£Ω90°„£¨
°ý°œPDG£Ω°œEPF£¨
°ý°˜PDG°’°˜EPF£®AAS£©£¨
°ýDG£ΩPF£¨
°þDG£ΩAF£Ωm©Å4£¨
°ýP£®m£¨m©Å4£©£¨
°þµ„P‘⁄∑¥±»¿˝∫Ø ˝y£Ω![]() £¨
£¨
°ým£®m©Å4£©£Ω16£¨
°ým£Ω2+2![]() ªÚm£Ω2©Å2
ªÚm£Ω2©Å2![]() £®…·£©£Æ
£®…·£©£Æ

°æƒø°øƒ≥–£ø™’π°∞◊þΩ¯÷–π˙ ˝—ß ∑°±Œ™÷˜Ã‚µƒ÷™ ∂æ∫»¸ªÓ∂Ø£¨∞À°¢æ≈ƒÍº∂∏˜”–200√˚—ß…˙≤Œº”æ∫»¸£¨Œ™¡ÀΩ‚’‚¡Ω∏ˆƒÍº∂≤Œº”æ∫»¸—ß…˙µƒ≥…º®«Èøˆ£¨¥”÷–∏˜Àʪ˙≥È»°20√˚—ß…˙µƒ≥…º®£¨ ˝æð»Áœ¬£∫
∞ÀƒÍº∂ | 91 | 89 | 77 | 86 | 71 | æ≈ƒÍº∂ | 84 | 93 | 66 | 69 | 76 |
51 | 97 | 93 | 72 | 91 | 87 | 77 | 82 | 85 | 88 | ||
81 | 92 | 85 | 85 | 95 | 90 | 88 | 67 | 88 | 91 | ||
88 | 88 | 90 | 64 | 91 | 96 | 68 | 97 | 99 | 88 |
’˚¿Ì…œ√Ê ˝æ𣨵√µΩ»Áœ¬Õ≥º∆±Ì£∫
≥…º® »À ˝ ƒÍº∂ |
|
|
|
|
|
∞ÀƒÍº∂ | 1 | 1 | 3 | 7 | 8 |
æ≈ƒÍº∂ | 0 | 4 | 2 | 8 | 6 |
—˘±æ ˝æðµƒ∆Ωæ˘ ˝°¢÷–Œª ˝°¢÷⁄ ˝°¢∑Ω≤Ó»Áœ¬±ÌÀ˘ æ£∫
Õ≥º∆±Ì ƒÍº∂ | ∆Ωæ˘ ˝ | ÷–Œª ˝ | ÷⁄ ˝ | ∑Ω≤Ó |
∞ÀƒÍº∂ | 83.85 | 88 | 91 | 127.03 |
æ≈ƒÍº∂ | 83.95 | 87.5 | | 99.45 |
∏˘æð“‘…œ–≈œ¢£¨ªÿ¥œ¬¡–Œ £∫
£®1£©–¥≥ˆ…œ±Ì÷–÷⁄ ˝![]() µƒ÷µ.
µƒ÷µ.
£®2£© ‘π¿º∆∞À°¢æ≈ƒÍº∂’‚¥Œ—°∞Œ≥…º®80∑÷“‘…œµƒ»À ˝∫Õ.
£®3£©ƒ„»œŒ™ƒƒ∏ˆƒÍº∂—ß…˙µƒæ∫»¸≥…º®Ωœ∫√£øÀµ√˜ƒ„µƒ¿Ì”….£®÷¡…Ÿ¥”¡Ω∏ˆ≤ªÕ¨µƒΩ«∂»Àµ√˜Õ∆∂œµƒ∫œ¿Ì–‘£©