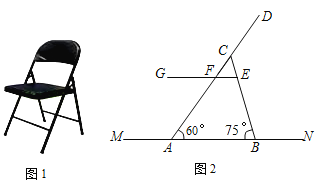
题目内容
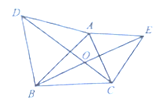
【题目】如图,矩形ABCD中,∠ABC=90,AB=6cm,BC=8cm,动点P从点C出发,在线段AC上以每秒5cm的速度向点A匀速运动,同时动点Q从点B出发,在BC边上以每秒4cm的速度向点C匀速运动,动点E从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(0<t<2).
(1)若△CDE与△ADC相似,求t的值.
(2)连接AQ,BP,CE,若BP⊥CE,求t的值;
(3)当PQ长度取得最小值时,求t的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)由题意可得CD2=DEDA,即36=4t×8,解方程即可.
(2)如图1中,作PM⊥BC于M.由△PMB∽△QBA,得![]() ,由CP=5t,CM=4t,PM=3t,可得方程
,由CP=5t,CM=4t,PM=3t,可得方程![]() ,解方程即可.
,解方程即可.
(3)根据PQ=![]() ,利用二次函数的性质即可解决问题.
,利用二次函数的性质即可解决问题.
试题解析:(1)∵0<t<2,
∴点E与点A不重合,
∵△CDE与△ADC相似,
∴∠DCE=∠DAC,
∴![]() ,
,
CD2=DEDA,即36=4t×8,
解得t=![]() s.
s.
(2)如图1,

∵DE=BQ=4t,AD=BC,AD∥BC
∴AE=CQ,AE∥CQ,
∴四边形AECQ为平行四边形,
∴CE∥AQ,过点P做PM⊥CB于点M,
∵BP⊥CE,CE∥AQ,
∴BP⊥AQ,
∴∠ABP+∠PBM=90°,∠BAQ+∠PBA=90°,
∴∠BAQ=∠PBM,∵∠ABQ=∠PMB=90°.
∴△PMB∽△QBA,
∴![]() ,
,
∵CP=5t,CM=4t,PM=3t,
∴![]() ,
,
所以t=![]() s.
s.
(3)如图2,
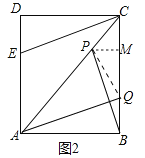
在Rt△PMQ中,PQ=![]() ,
,
所以当t=-![]() s时,PQ可以取得最小值.
s时,PQ可以取得最小值.

【题目】为弘扬中华传统文化,某校组织七年级800名学生参加诗词大赛,为了解学生整体的诗词积累情况,随机抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,请根据尚未完成的列图表,解答问题:
组别 | 分数段 | 频数 | 频率 |
一 | 50.5~60.5 | 16 | 0.08 |
二 | 60.5~70.5 | 40 | 0.20 |
三 | 70.5~80.5 | 50 | 0.25 |
四 | 80.5~90.5 | m | 0.35 |
五 | 90.5~100.5 | 24 | n |
(1)本次抽样中,表中m=____,n=____,样本成绩的中位数落在第____组内.
(2)补全频数分布直方图.
(3)若规定成绩超过80分为优秀,请估计该校七年级学生中诗词积累成绩为优秀的人数.