题目内容
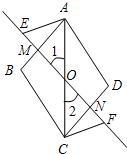 56、如图,O为平行四边形ABCD的对角线AC的中点,过点O作一条直线分别与AB,CD交于点M,N,点E,F在直线MN上,且OE=OF.
56、如图,O为平行四边形ABCD的对角线AC的中点,过点O作一条直线分别与AB,CD交于点M,N,点E,F在直线MN上,且OE=OF.(1)图中共有几对全等三角形,请把它们都写出来;
(2)求证:∠MAE=∠NCF.
分析:(1)单个三角形全等的是:△AMO≌△CNO,△AME≌△CNF.由2部分组成全等的是:△OCF≌△OAE,△ABC≌△CDA;
(2)由题中已知条件可证得△OCF≌△OAE,进而求得∠EAO=∠FCO,而后利用平行四边形的对边平行的性质求得相应的内错角相等,进而求解.
(2)由题中已知条件可证得△OCF≌△OAE,进而求得∠EAO=∠FCO,而后利用平行四边形的对边平行的性质求得相应的内错角相等,进而求解.
解答:解:(1)有4对全等三角形.
分别为△AMO≌△CNO,△OCF≌△OAE,△AME≌△CNF,△ABC≌△CDA;
(2)证明:∵OA=OC,∠1=∠2,OE=OF,
∴△OCF≌△OAE.
∴∠EAO=∠FCO.
在平行四边形ABCD中,AB∥CD,
∴∠BAO=∠DCO.
∴∠EAM=∠NCF.
分别为△AMO≌△CNO,△OCF≌△OAE,△AME≌△CNF,△ABC≌△CDA;
(2)证明:∵OA=OC,∠1=∠2,OE=OF,
∴△OCF≌△OAE.
∴∠EAO=∠FCO.
在平行四边形ABCD中,AB∥CD,
∴∠BAO=∠DCO.
∴∠EAM=∠NCF.
点评:找三角形全等应有规律的去找,先找单个的全等三角形,再找由2部分或2部分以上组成全等的三角形.本题的难点在于利用平行四边形的对边平行的性质得到一组内错角相等.

练习册系列答案
相关题目
 如图,E为平行四边形ABCD中BC边的中点,AE交对角线BD于G,如果△BEG的面积是1,则平行四边形ABCD的面积是
如图,E为平行四边形ABCD中BC边的中点,AE交对角线BD于G,如果△BEG的面积是1,则平行四边形ABCD的面积是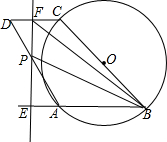 如图,ABCD为平行四边形,以BC为直径的⊙O经过点A,∠D=60°,BC=2,一动点P在AD上移动,过点P作直线AB的垂线,分别交直线AB、CD于E、F,设点O到EF的距离为t,若B、P、F三点能构成三角形,设此时△BPF的面积为S.
如图,ABCD为平行四边形,以BC为直径的⊙O经过点A,∠D=60°,BC=2,一动点P在AD上移动,过点P作直线AB的垂线,分别交直线AB、CD于E、F,设点O到EF的距离为t,若B、P、F三点能构成三角形,设此时△BPF的面积为S.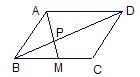 14、如图:M为平行四边形ABCD的BC边的中点,AM交BD于点P,若PM=4,则AP=
14、如图:M为平行四边形ABCD的BC边的中点,AM交BD于点P,若PM=4,则AP= (2013•安徽)如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=2,则S1+S2=
(2013•安徽)如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=2,则S1+S2=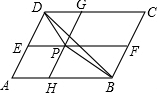 (1)已知|2011-x|+
(1)已知|2011-x|+