题目内容
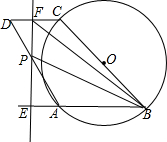 如图,ABCD为平行四边形,以BC为直径的⊙O经过点A,∠D=60°,BC=2,一动点P在AD上移动,过点P作直线AB的垂线,分别交直线AB、CD于E、F,设点O到EF的距离为t,若B、P、F三点能构成三角形,设此时△BPF的面积为S.
如图,ABCD为平行四边形,以BC为直径的⊙O经过点A,∠D=60°,BC=2,一动点P在AD上移动,过点P作直线AB的垂线,分别交直线AB、CD于E、F,设点O到EF的距离为t,若B、P、F三点能构成三角形,设此时△BPF的面积为S.(1)计算平行四边形ABCD的面积;
(2)求S关于t的函数关系式,并写出自变量t的取值范围;
(3)△BPF的面积存在最大值吗?若存在,请求出这个最大值,若不存在,请说明理由.
分析:(1)要求平行四边形ABCD的面积,已知底边AB,再需证明AC为平行四边形ABCD底边AB上的高即可,并求得AC的大小.因此根据圆O为△ABC外接圆,BC为圆O的直径,可得到AC⊥AB;根据∠D的大小得到∠B的大小.在Rt△ABC中,根据边角间的关系可求得AC、AB的值.进而求得平行四边形ABCD的面积.
(2)作OH⊥AB于点H,由(1)和垂径定理知BH的大小.要求△BPF的面积为S,需求底边PF的值与高EB的值.要求PF的值可根据∠D与FD来求得,进一步需求得CD与FC的大小,通过AB=CD、EA=FC,均用t来表示.而EB=EH+BH,也用t来表示,代入三角形面积公式即可.
(3)根据(2)中得出的函数式,利用配方法根据t的取值范围,求得最大值.
(2)作OH⊥AB于点H,由(1)和垂径定理知BH的大小.要求△BPF的面积为S,需求底边PF的值与高EB的值.要求PF的值可根据∠D与FD来求得,进一步需求得CD与FC的大小,通过AB=CD、EA=FC,均用t来表示.而EB=EH+BH,也用t来表示,代入三角形面积公式即可.
(3)根据(2)中得出的函数式,利用配方法根据t的取值范围,求得最大值.
解答: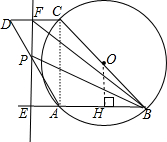
解:(1)连接AC,
∵BC为直径,
∴AC⊥AB,
在平行四边形ABCD中,
∵∠D=60°,BC=2,
∴∠ABC=∠D=60°,AD=BC=2,
∴AB=
BC=1,
由勾股定理,得AC=
,
∴S△ABCD=AB•AC=
;
(2)作OH⊥AB于点H,
由(1)和垂径定理知BH=
,
∵O到EF的距离为t,
∴BE=t+
,
在矩形ACFE中,CF=AE,AC=EF=
,
∵AE=t+
-1=t-
,
∴CF=t-
,
在平行四边形ABCD中,CD=AB=1,
∴DF=CD-CF=1-(t-
)=
-t,
∵
=tan60°,
∴PF=
(
-t),
∴S=
PF•BE=
(t+
)•
(
-t)=
(-t2-
t+
t+
)=-
t2+
t+
(
≤t≤
);
(3)存在,由(2)知S=-
t2+
t+
(
≤t≤
),
得S=-
(t-
)2 +
(
≤t≤
),
∴当t=
时,S有最大值
.
答:(1)平行四边形ABCD的面积为
;(2)S关于t的函数关系式为-
t2+
t+
,自变量x的取值范围为
≤t≤
;(3)△BPF的面积存在最大值,当t=
时,S有最大值
.

解:(1)连接AC,
∵BC为直径,
∴AC⊥AB,
在平行四边形ABCD中,
∵∠D=60°,BC=2,
∴∠ABC=∠D=60°,AD=BC=2,
∴AB=
| 1 |
| 2 |
由勾股定理,得AC=
| 3 |
∴S△ABCD=AB•AC=
| 3 |
(2)作OH⊥AB于点H,
由(1)和垂径定理知BH=
| 1 |
| 2 |
∵O到EF的距离为t,
∴BE=t+
| 1 |
| 2 |
在矩形ACFE中,CF=AE,AC=EF=
| 3 |
∵AE=t+
| 1 |
| 2 |
| 1 |
| 2 |
∴CF=t-
| 1 |
| 2 |
在平行四边形ABCD中,CD=AB=1,
∴DF=CD-CF=1-(t-
| 1 |
| 2 |
| 3 |
| 2 |
∵
| PE |
| DF |
∴PF=
| 3 |
| 3 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 8 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
(3)存在,由(2)知S=-
| ||
| 2 |
| ||
| 2 |
| 3 |
| 8 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
得S=-
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴当t=
| 1 |
| 2 |
| ||
| 2 |
答:(1)平行四边形ABCD的面积为
| 3 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 8 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
点评:本题着重考查了二次函数解析式、平行四边形的性质、垂径定理、勾股定理、探究二次函数求极值等重要知识点,综合性强,能力要求极高.考查数形结合的数学思想方法.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 23、如图,ABCD为平行四边形,DFEC和BCGH为正方形.求证:AC⊥EG.
23、如图,ABCD为平行四边形,DFEC和BCGH为正方形.求证:AC⊥EG.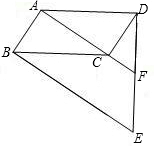 如图,ABCD为平行四边形,BE∥AC,DE交AC延长线于F点,交BE于E点.
如图,ABCD为平行四边形,BE∥AC,DE交AC延长线于F点,交BE于E点.