题目内容
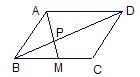14、如图：M为平行四边形ABCD的BC边的中点，AM交BD于点P，若PM=4，则AP=8
．分析：首先由平行四边形的性质可知BC∥AD，然后证明△BMP∽△DAP，再根据相似三角形的对应边成比例，得出AP：PM=AD：BM，从而求出AP的长度．
解答：解：∵四边形ABCD是平行四边形，
∴BC∥AD，AD=BC，
∴∠PBM=∠PDA，∠PMB=∠PAD，
∴△BMP∽△DAP，
∴AP：PM=AD：BM，
又∵M为BC边的中点，
∴BC=2BM，
∴AD=2BM，
∴AP=2PM=8．
∴BC∥AD，AD=BC，
∴∠PBM=∠PDA，∠PMB=∠PAD，
∴△BMP∽△DAP，
∴AP：PM=AD：BM，
又∵M为BC边的中点，
∴BC=2BM，
∴AD=2BM，
∴AP=2PM=8．
点评：本题主要考查了相似三角形的判定及性质．有两角对应相等的两个三角形相似．相似三角形的对应边成比例．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
如图，E为平行四边形ABCD中BC边的中点，AE交对角线BD于G，如果△BEG的面积是1，则平行四边形ABCD的面积是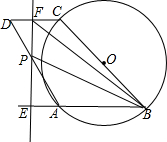
如图，ABCD为平行四边形，以BC为直径的⊙O经过点A，∠D=60°，BC=2，一动点P在AD上移动，过点P作直线AB的垂线，分别交直线AB、CD于E、F，设点O到EF的距离为t，若B、P、F三点能构成三角形，设此时△BPF的面积为S．
（2013•安徽）如图，P为平行四边形ABCD边AD上一点，E、F分别为PB、PC的中点，△PEF、△PDC、△PAB的面积分别为S、S1、S2，若S=2，则S1+S2=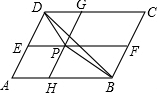
（1）已知|2011-x|+