题目内容
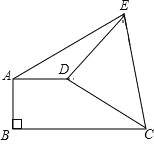
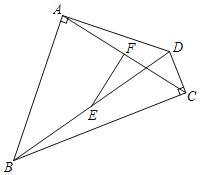
【题目】如图,四边形ABCD中,∠BAD=90°,∠DCB=90°,E、F分别是BD、AC的中点.
(1)请你猜想EF与AC的位置关系,并给予证明;
(2)当AC=16,BD=20时,求EF的长.
【答案】(1) EF⊥AC,见解析;(2)EF=6
【解析】
(1)结论:EF⊥AC.利用直角三角形斜边中线以及等腰三角形的性质即可解决问题.
(2)在Rt△ECF中,利用勾股定理即可解决问题.
(1)EF⊥AC.理由如下:
连接AE、CE,
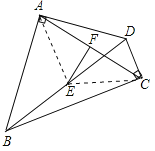
∵∠BAD=90°,E为BD中点,
∴AE=![]() DB,
DB,
∵∠DCB=90°,
∴CE=![]() BD,
BD,
∴AE=CE,
∵F是AC中点,
∴EF⊥AC;
(2)∵AC=16,BD=20,E、F分别是边AC、BD的中点,
∴AE=CE=10,CF=8,
∵EF⊥AC.
∴EF=![]() =
=![]() =6.
=6.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目