题目内容
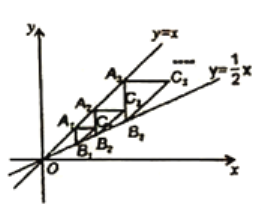
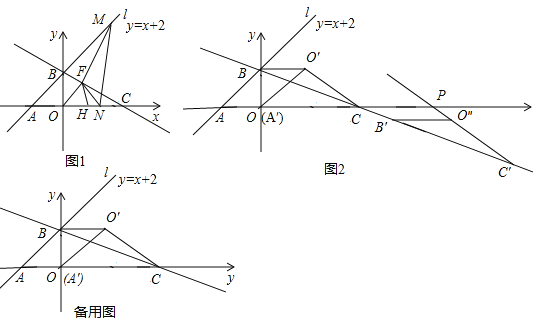
【题目】如图1,在平面直角坐标系中,直线l:y=x+2与x轴交于点A,与y轴交于点B,点C在x轴的正半轴上,且OC=2OB.
(1)点F是直线BC上一动点,点M是直线AB上一动点,点H为x轴上一动点,点N为x轴上另一动点(不与H点重合),连接OF、FH、FM、FN和MN,当OF+FH取最小值时,求△FMN周长的最小值;
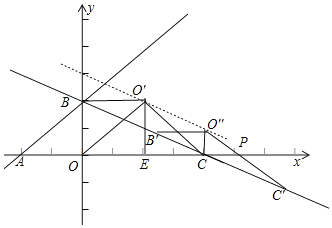
(2)如图2,将△AOB绕着点B逆时针旋转90°得到△A′O′B,其中点A对应点为A′,点O对应点为O',连接CO',将△BCO'沿着直线BC平移,记平移过程中△BCO'为△B'C'O″,其中点B对应点为B',点C对应点为C',点O′对应点为O″,直线C'O″与x轴交于点P,在平移过程中,是否存在点P,使得△O″PC为等腰三角形?若存在请直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)满足条件的点P为:(8+2
;(2)满足条件的点P为:(8+2![]() ,0)或(
,0)或(![]() ,0)或(5,0)
,0)或(5,0)
【解析】
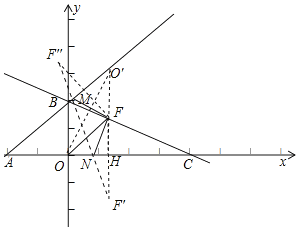
(1)先求出点A,点B坐标,用待定系数法求出直线BC的解析式,作点O关于直线BC的对称点O'(![]() ),过点O'作O'H⊥OC于点F,交BC于点H,此时OF+FH的值最小,求出点F坐标,作点F关于直线AB与直线OC的对称点,连接F'F'交直线AB于点M,交直线OC于点N,此时△FMN周长有最小值,由两点距离公式可求△FMN周长的最小值;
),过点O'作O'H⊥OC于点F,交BC于点H,此时OF+FH的值最小,求出点F坐标,作点F关于直线AB与直线OC的对称点,连接F'F'交直线AB于点M,交直线OC于点N,此时△FMN周长有最小值,由两点距离公式可求△FMN周长的最小值;
(2)分O'C=PC,O'P=PC,O'P=O'C三种情况讨论,由等腰三角形的性质可求解.
解:(1)∵直线y=x+2与x轴交于点A,与y轴交于点B,
∴当x=0时,y=2,
当y=0时,x=﹣2,
∴点A(﹣2,0),点B(0,2)
∴OB=2
∵OC=2OB.
∴OC=4
∴点C(4,0)
设直线BC解析式为:y=kx+2,且过点C(4,0)
∴0=4k+2
∴k=![]()
∴直线BC解析式为:y=![]() x+2,
x+2,
如图,作点O关于直线BC的对称点O'(![]() ),过点O'作O'H⊥OC于点F,交BC于点H,此时OF+FH的值最小.
),过点O'作O'H⊥OC于点F,交BC于点H,此时OF+FH的值最小.
∴点F的横坐标为![]()
∴点F(![]() )
)
作点F关于直线OC的对称点F'(![]() ),
),
作点F关于直线AB的对称点F'(![]() )
)
连接F'F'交直线AB于点M,交直线OC于点N,此时△FMN周长有最小值,
∴△FMN周长的最小值=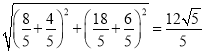
(2)∵将△AOB绕着点B逆时针旋转90°得到△A'O’B,
∴O'点坐标(2,2)
设直线O'C的解析式为:y=mx+b
∴![]()
∴![]()
∴直线O'C的解析式为:y=﹣x+4
如图,过点O'作O'E⊥OC
∴OE=2,O'E=2
∴EC=O'E=2
∴∠O'CE=45°
∵将△BCO'沿着直线BC平移,
∴O'O'∥BC,O'C∥O'C',
∴设O'O'的解析式为y=![]() x+n,且过(2,2)
x+n,且过(2,2)
∴2=![]() ×2+n
×2+n
∴n=3
∴直线O'O'的解析式为y=![]() x+3
x+3
若CO'=CP,
∵O'C∥O'C',
∴∠O'CE=∠O'PC=45°
∵CO'=CP
∴∠CO'P=∠O'PC=45°
∴∠O'CP=90°
∴点O'的横坐标为4,
∴当x=4时,y=![]() ×4+3=1
×4+3=1
∴点O'(4,1)
∴CO'=1=CP
∴点P(5,0)
若CO'=O'P,如图,过点O'作O'N⊥CP于N,

∵O'C∥O'C',
∴∠O'CE=∠O'PC=45°
∵CO'=O'P
∴∠O'CP=∠CPO'=45°,
∴∠CO'P=90°,且CO'=O'P,O'N⊥CP
∴CN=PN=O'N=![]() CP
CP
设CP=a,
∴CN=PN=O'N=![]() CP=
CP=![]() a
a
∴点O'(4+![]() a,
a,![]() a),且直线O'O'的解析式为y=﹣
a),且直线O'O'的解析式为y=﹣![]() x+3
x+3
∴![]() a=﹣
a=﹣![]() (4+
(4+![]() a)+3
a)+3
∴a=![]()
∴CP=![]()
∴点P(![]() ,0)
,0)
若CP=O'P,如图,过点O'作O'N⊥CP于N

∵O'C∥O'C',
∴∠O'CE=∠O'PM=45°
∴∠O'PN=∠O'PM=45°,且O'N⊥CP
∴∠NPO'=∠PO'N=45°
∴PN=O'N
∴O'P=![]() PN=CP
PN=CP
设PN=b,则O'N=b,CP=PO'=![]() b
b
∴点O'坐标(4+![]() b+b,﹣b),且直线O'O'的解析式为y=
b+b,﹣b),且直线O'O'的解析式为y=![]() x+3
x+3
∴﹣b=![]() ×(4+
×(4+![]() b+b)+3
b+b)+3
∴b=2![]() +2
+2
∴CP=4+2![]()
∴点P坐标(8+2![]() ,0)
,0)
综上所述:满足条件的点P为:(8+2![]() ,0)或(
,0)或(![]() ,0)或(5,0)
,0)或(5,0)

 名校课堂系列答案
名校课堂系列答案【题目】用A4纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元.
设在同一家复印店一次复印文件的页数为x(x为非负整数).
(1)根据题意,填写下表:
一次复印页数(页) | 5 | 10 | 20 | 30 | … |
甲复印店收费(元) | 0.5 |
| 2 |
| … |
乙复印店收费(元) | 0.6 |
| 2.4 |
| … |
(2)设在甲复印店复印收费y1元,在乙复印店复印收费y2元,分别写出y1,y2关于x的函数关系式;
(3)当x>70时,顾客在哪家复印店复印花费少?请说明理由.