题目内容
【题目】如图,已知△ABC.利用直尺和圆规,根据下列要求作图(不写作法,保留作图痕迹),并回答问题.
(1)作∠ABC的平分线BD、交AC于点D;
(2)作线段BD的垂直平分线,交AB于点E,交BC于点F,连接DE,DF;
(3)写出你所作出的图形中的相等线段.
【答案】(1)射线BD即为所求.见解析;(2)直线BD即为所求.见解析;(3)EB=ED=FD=FB,BO=DO,EO=FO.
【解析】
(1)根据尺规作角平分线即可完成
(2)根据线段垂直平分线的性质即可
(3)根据线段垂直平分线的性质和全等三角形的知识即可找到相等的线段
(1)射线BD即为所求.
(2)直线BD即为所求.
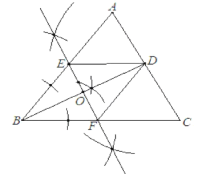
(3)记EF与BD的交点为O.
因为EF为BD的垂直平分线,
所以EB=ED,FB=FD,BO=DO,∠EOB=∠FOB=90°.
因为BD为∠ABC的角平分线,
所以∠ABD=∠CBD.
因为∠ABD=∠CBD,BO=BO,∠EOB=∠FOB=90°,
所以△EOB≌△FOB(ASA).
所以EO=FO,BE=BF.
因为EB=ED,FB=FD,BE=BF,
所以EB=ED=FD=FB.
因此,图中相等的线段有:EB=ED=FD=FB,BO=DO,EO=FO.

练习册系列答案
相关题目