题目内容
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,点
,点![]() 是
是![]() 轴上两点,其中
轴上两点,其中![]() ,点
,点![]() 都在
都在![]() 轴上,
轴上,![]() 在射线
在射线![]() 上(不与点
上(不与点![]() 重合),
重合),![]() ,连结
,连结![]() .
.
(1)求![]() 、
、![]() 的坐标;
的坐标;
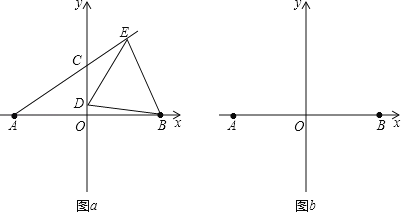
(2)如图![]() ,若
,若![]() 在
在![]() 轴正半轴,
轴正半轴,![]() 在线段
在线段![]() 上,当
上,当![]() 时,求证:
时,求证:![]() 为等边三角形;(提示:连结
为等边三角形;(提示:连结![]() )
)
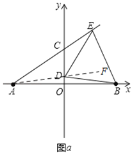
(3)当![]() 时,在图
时,在图![]() 中画出示意图,设
中画出示意图,设![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(1) A(﹣4,0),B(4,0);(2)见解析;(3) 10或6
【解析】
(1)由a2+2ab+b2+|b-4|=0,得出(a+b)2+|b-4|=0,再根据非负数的性质,得出a=-4,b=4,即可得到A(-4,0),B(4,0);
(2)连接AD并延长至F,根据等腰三角形的性质以及三角形外角性质,即可得出∠BDF=∠DAO+∠DBO=2∠DAO,∠EDF=2∠DAE,进而得到∠EDB=60°,再根据DE=DB,即可得出△BDE为等边三角形;
(3)分两种情况进行讨论:①当C在y轴正半轴时,②当C在y轴负半轴时,分别判定全等三角形,根据全等三角形的对应边相等,分别求得n-m=4,m+n=-4,再根据mn=2,求得![]() 的值即可.
的值即可.
解:(1)∵a2+2ab+b2+|b﹣4|=0,∴(a+b)2+|b﹣4|=0,
又∵(a+b)2≥0,|b﹣4|≥0,∴(a+b)2=0,|b﹣4|=0,
∴a=﹣4,b=4,∴A(﹣4,0),B(4,0);
(2)证明:如图a,连接AD并延长至F,
∵A(﹣4,0),B(4,0),∴OA=OB,∵OD⊥AB,∴DA=DB,
∴∠DAO=∠DBO,∴∠BDF=∠DAO+∠DBO=2∠DAO,∵DA=DB,DE=DB,
∴DA=DE,同理可得∠EDF=2∠DAE,
∴∠BDF+∠EDF=2∠DAE+2∠DAO=2∠CAO=60°,即∠EDB=60°,
又∵DE=DB,∴△BDE为等边三角形;
(3)分两种情况:
①当C在y轴正半轴时,如图b所示,过点E作EG⊥y轴于点G,
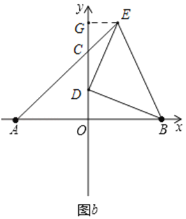
则∠GED+∠GDE=90°,∵DE⊥DB,∴∠ODB+∠GDE=90°,∴∠GED=∠ODB,
又∵∠DGE=∠DOB=90°,DE=DB,
∴在△DGE和△BOD中,
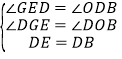 ,
,
∴△DGE≌△BOD(AAS)
∴OD=EG,DG=OB=4,
∵E(m,n),
∴OD=EG=m,OG=n,
由OG﹣OD=DG,得n﹣m=4,
∵mn=2,
∴![]() =10;
=10;
②当C在y轴负半轴时,如图c所示,过点E作EG⊥y轴于点G,
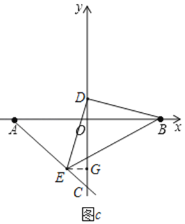
同理可得,△DGE≌△BOD,
∴OD=EG,DG=OB=4,
∵E(m,n),
∴OD=EG=﹣m,OG=﹣n,
由OD+OG=DG,得﹣m+(﹣n)=4,则m+n=﹣4,
∵mn=2,
∴![]() =6,
=6,
综上所述,![]() 的值为10或6.
的值为10或6.