题目内容
【题目】如图,将一个边长为![]() 的正方形图形分割成四部分,观察图形,解答下列问题:
的正方形图形分割成四部分,观察图形,解答下列问题:
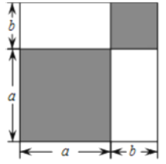
(1)根据图中条件,请用两种方法表示该阴影图形的总面积
方法1:_________________方法2__________________;
由此可得等量关系:______________________________;
应用该等量关系解决下列问题:
(2)若图中的a,b(![]() )满足
)满足![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;
;![]() ;
;![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]()
【解析】
(1)根据图形和图形中的数据可以用代数式表示出阴影部分的面积;
(2)根据题意和(1)中的结果可以求得a+b的值;
(3)根据a24a+1=0,通过变形可以求得所求式子的值.
(1)由题意可得,
阴影图形的总面积方法1:a2+b2,方法2:(a+b)22ab,
∴a2+b2=(a+b)22ab,
故答案为:a2+b2;(a+b)22ab;a2+b2=(a+b)22ab;
(2)∵a,b(a>b)满足a2+b2=38,ab=13,
∴38=(a+b)22×13,
解得,a+b=8或a+b=8(舍去),
即a+b的值是8;
(3)∵a24a+1=0,
∴a4+![]() =0,
=0,
∴a+![]() =4,
=4,
∴(a+![]() )2=16,
)2=16,
∴a2+2+![]() =16,
=16,
∴a2+![]() =14.
=14.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目