题目内容
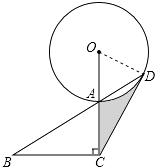
【题目】如图,已知在Rt△ABC中,∠B=30°,∠ACB=90°,延长CA到O,使AO=AC,以O为圆心,OA长为半径作⊙O交BA延长线于点D,连接CD.
(1)求证:CD是⊙O的切线;
(2)若AB=4,求图中阴影部分的面积.
【答案】
(1)证明:连接OD,
∵∠BCA=90°,∠B=30°,
∴∠OAD=∠BAC=60°,
∵OD=OA,
∴△OAD是等边三角形,
∴AD=OA=AC,∠ODA=∠O=60°,
∴∠ADC=∠ACD= ![]() ∠OAD=30°,
∠OAD=30°,
∴∠ODC=60°+30°=90°,
即OD⊥DC,
∵OD为半径,
∴CD是⊙O的切线
(2)解:∵AB=4,∠ACB=90°,∠B=30°,
∴OD=OA=AC= ![]() AB=2,
AB=2,
由勾股定理得:CD= ![]() =
= ![]() =2
=2 ![]() ,
,
∴S阴影=S△ODC﹣S扇形AOD= ![]() ×2×2
×2×2 ![]() ﹣
﹣ ![]() =2
=2 ![]() ﹣
﹣ ![]() π.
π.
【解析】(1)证明切线须连半径,证直线和半径垂直;(2) 阴影部分的面积可转化为三角形面积减去扇形面积.
【考点精析】本题主要考查了含30度角的直角三角形和勾股定理的概念的相关知识点,需要掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目