Question

【题目】某工厂有一种材料，可加工甲、乙、丙三种型号机械配件共240件，厂方计划由20个工人一天内加工完成，并要求每人只加工一种配件，根据下表提供的信息，解答下列问题：

配件种类	甲	乙	丙
每人可加工配件的数量（个）	16	12	10
每个配件获利（元）	6	8	5

（1）设加工甲种配件的人数为x，加工乙种配件的人数为y，求y与x之间的函数关系式

（2）如果加工每种配件的人数均不少于3人，那么加工配件的人数安排方案有几种？并写出每种安排方案

（3）要使此次加工配件的利润最大，应采用哪种方案？最大利润是多少？

Answer 1

【答案】1）y=-3x＋20 （2）有三种方案, 甲、乙、丙依次为：3,11,6或4,8,8或5,5,10.

（3）W=-92x＋1920，x=3时，W有最大值1644元

【解析】

（1）根据图表得出16x+12y+10（20-x-y）=240，从而求出y与x的关系式即可；

（2）利用（1）中关系式即可得出方案；

（3）分别求出（2）中方案的利润即可．

解：（1）依题意得

16x+12y+10（20-x-y）=240

y=-3x+20

∴y与x的函数关系是：y=-3x+20

（2）设加工丙种配件的人数为z=（20-x-y）人，

依题意得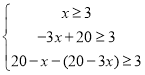

解得：
所以当x=3时，y=-3×3+20=11，z=20-3-11=6，
当x=4时，y=8，z=8，
当x=5时，y=5，z=10，
其他都不符合题意，
∴加工配件的人数安排方案有三种；

（3）设此次销售利润为W元.

W=16x·6+12(20-3x)·8+10·2x·5

=-92x+1920

∵W随x的增大而减小

∴x=3时 W最大=1644元

∴要获利最大，应采用（2）中的方案①，最大利润为1644元.