题目内容
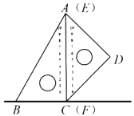
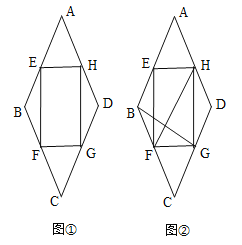
【题目】在菱形ABCD中,∠A=60°,AB=8cm,如图①,点E,H从点A开始向B,D运动,同时点F,G从点C向B,D运动,运动速度都为1cm/秒,运动时间为t秒(0≤t<8).
(1)当运动时间t=4时,求证:四边形EFGH为矩形;
(2)当t等于多少秒时,四边形EFGH面积是菱形ABCD面积的![]() ;
;
(3)如图②,连接HF,BG,当t等于多少秒时,HF⊥BG.
【答案】(1)见解析;(2) t=![]() ;(3)t=4.
;(3)t=4.
【解析】
(1)根据t=4时,E、F、G、H分别是AB、BC、CD、AD的中点,可证四边形EFGH为矩形;
(2)先证明四边形EFGH为矩形,然后根据∠ADB=60°求出HG=![]() ,由四边形EFGH面积是菱形ABCD面积的
,由四边形EFGH面积是菱形ABCD面积的![]() 列方程求解即可;
列方程求解即可;
(3)延长GF,过点B作BM⊥FG交点M,由(2)可知,FG=t, HG=![]() ,证明
,证明![]() ∽
∽![]() ,根据相似三角形的对应边成比例列出比例式,在含30°的直角三角形BMF中求出BM、FM,代入比例式即可求出t值.
,根据相似三角形的对应边成比例列出比例式,在含30°的直角三角形BMF中求出BM、FM,代入比例式即可求出t值.
解:(1)连接AC、BD,如图:
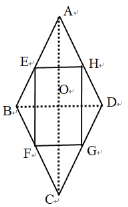
当t=4时,AE=AH=CF=CG=4
![]() 在菱形ABCD中,AB=BC=CD=AD=8,AC⊥BD
在菱形ABCD中,AB=BC=CD=AD=8,AC⊥BD
![]() E、F、G、H分别是AB、BC、CD、AD的中点
E、F、G、H分别是AB、BC、CD、AD的中点
![]() EH∥BD,FG∥BD,EF∥AC,HG∥AC
EH∥BD,FG∥BD,EF∥AC,HG∥AC
![]() EH∥FG,EF∥HG
EH∥FG,EF∥HG ![]() EH∥BD,FG∥BD
EH∥BD,FG∥BD
![]() 四边形EFGH为平行四边形
四边形EFGH为平行四边形
![]() EH∥BD,EF∥AC,AC⊥BD
EH∥BD,EF∥AC,AC⊥BD
![]() EH⊥RF
EH⊥RF
![]() 四边形EFGH为矩形;
四边形EFGH为矩形;
(2)由(1)中图可知AE=AH=CF=CG=t,则BE=DH=BF=DG=8-t
![]() 在菱形ABCD中,AB=BC=CD=AD=8,AC⊥BD,∠A=60°,
在菱形ABCD中,AB=BC=CD=AD=8,AC⊥BD,∠A=60°,
![]() EH=t,∠ADB=60°,
EH=t,∠ADB=60°,
![]() ,∠A=∠A ,
,∠A=∠A ,
![]()
![]()
![]()
![]()
![]() EH∥BD
EH∥BD
同理可得:FG∥BD,EF∥AC,HG∥AC,
![]() EH∥FG,EF∥HG,
EH∥FG,EF∥HG,
![]() EH∥BD,FG∥BD
EH∥BD,FG∥BD
![]() 四边形EFGH为平行四边形
四边形EFGH为平行四边形
![]() EH∥BD,EF∥AC,AC⊥BD,
EH∥BD,EF∥AC,AC⊥BD,
![]() EH⊥EF,
EH⊥EF,
![]() 四边形EFGH为矩形,
四边形EFGH为矩形,
![]() ∠ADB=60°,BD⊥HG,
∠ADB=60°,BD⊥HG,
![]() HG=
HG=![]()
![]() 四边形EFGH面积是菱形ABCD面积的
四边形EFGH面积是菱形ABCD面积的![]() ,
,
![]() t·
t·![]() =
=![]() ·
·![]() ·8·
·8·![]()
解得 t=![]() ,
,
![]() 当t=
当t=![]() 时,四边形EFGH面积是菱形ABCD面积的
时,四边形EFGH面积是菱形ABCD面积的![]() ;
;
(3)延长GF,过点B作BM⊥FG交点M,
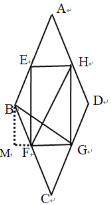
由(2)可知,FG=t,BF=8-t,HG=![]() ,四边形EFGH为矩形,HF⊥BG
,四边形EFGH为矩形,HF⊥BG
![]() ∠FHG+∠HFG=90°,∠FGB+∠HFG=90°
∠FHG+∠HFG=90°,∠FGB+∠HFG=90° ![]() ∠FHG=∠FGB
∠FHG=∠FGB
又∠FGH=∠FMB,
![]() ∽
∽![]()
![]() ,
,
![]()
![]()
![]()
![]()
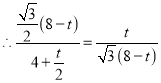
化简得![]()
解得t=4或t=24(舍去)
![]() 当t=4时,HF⊥BG.
当t=4时,HF⊥BG.