题目内容
【题目】如图,□ABCD中,AE⊥BD于点E,CF⊥BD于点F.
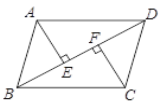
(1)求证:BF=DE;
(2)如果∠ABC=75°, ∠DBC=30°,BC=2,求BD的长.
【答案】(1)证明见解析;(2)![]() +1.
+1.
【解析】
(1)根据矩形的性质和已知条件证得△ADE≌△CBF,再利用全等三角形的性质即可证明;
(2)先根据矩形的性质、勾股定理等知识求得AE的长,进而求得DE和BD的长.
(1)证明:∵□ABCD,
∴AD∥BC,AD=BC.
∴∠ADE=∠CBF.
∵AE⊥BD于点E,CF⊥BD于点F,
∴∠AED=∠CFB=90°.
在△ADE和△CBF中,
∠AED=∠BFC,∠ADE=∠CBF,|AD=BC
∴△ADE≌△CBF(AAS)
∴DE=BF
(2)解:∵∠ABC=75°,∠DBC=30°,
∴∠ABE=750-30°=45.
∵AB∥CD,
∴∠ABE=∠BDC=45°,
∵AD=BC=2, ∠ADE=∠CBF=30°,
∴在Rt△ADE中,AE=1,DE=![]() =
=![]() .
.
在Rt△AEB中,∠ABE=∠BAE=45°
故AE=BE=1.则BD=![]() +1.
+1.

练习册系列答案
相关题目