题目内容
【题目】如图,矩形ABCD中,AB=8,AD=10.
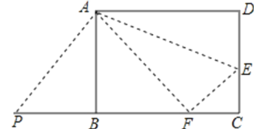
(1)E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处.求DE的长;
(2)点P是线段CB延长线上的点,连接PA,若△PAF是等腰三角形,求PB的长;
(3)M是AD上的动点,在DC上存在点N,使△MDN沿折痕MN折叠,点D落在BC边上点T处,请直接写出线段CT长度的最大值与最小值.
【答案】(1)5;(2)6或4或![]() ;(3)12.
;(3)12.
【解析】
(1)根据折叠的特点和勾股定理即可求出ED的长;
(2)需分AP=AF;PF=AF和AP=PF三种情况分别求出PB的长即可;
(3)由题意可知当点N与C重合时,CT取最大值是8;当点M与A重合时,CT取最小值为4,进而求出线段CT长度的最大值与最小值之和.
解:(1)∵四边形ABCD是矩形,AB=8,AD=10
∴AF=AD=10,FE=DE(折叠对称性)
∵在Rt△ABF中,BF=6,AF=10
∴FC=4
所以在Rt△ECF中,42+(8-DE)2=EF2,
∴DE=5;
(2)当AP=AF时,AB⊥PF,∴PB=BF=6;
当PF=AF时,则PB+6=10,解得PB=4;
若AP=PF,在Rt△APB中,AP2=PB2+AB2,解得PB=![]() .
.
综合可得PB=6或4或![]() ;
;
(3)当点N与C重合时,CT最大=MD=8;
当点M与A重合时,AT=AD=10,AB=8,CT最小=10-6=4,
∴线段CT长度的最大值与最小值之和为12.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某学习小组在研究函数y=![]() x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
(1)请补全函数图象;
(2)方程![]() x3﹣2x=﹣2实数根的个数为 ;
x3﹣2x=﹣2实数根的个数为 ;
(3)观察图象,写出该函数的两条性质.

【题目】二次函数y= ax+bx+c,自变量x 与函数y 的对应值如表:
x | ... | -5 | -4 | -3 | -2 | -1 | 0 | ... |
y | ... | 4 | 0 | -2 | -2 | 0 | 4 | ... |
下列说法正确的是( )
A. 抛物线的开口向下 B. 当x>-3时,y随x的增大而增大
C. 二次函数的最小值是-2 D. 抛物线的对称轴是x=-5/2