题目内容
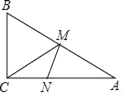
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=4,M是AB边上一动点,N是AC边上的一动点,则MN+MC的最小值为_____.
【答案】2![]()
【解析】分析: 作点C关于AB的对称点C′,过点C作C′N⊥AC于N,交AB于点M,则C′N的长即为MN+MC的最小值;
详解: 作点C关于AB的对称点C′,过点C作C′N⊥AC于N,交AB于点M,则C′N的长即为MN+MC的最小值,连接CC′交AB于点H,则CC′⊥AB,C′H=HC′,
∵∠C′MH=∠AMN,∠A=30°,
∴∠C′=∠A=30°,
∵AC=4,
∴HC=![]() AC,
AC,
∴CC′=4,
∴C′N=CC′cosC′=2![]() .
.
故答案为2![]() .
.
点睛:本题考查轴对称最短问题,直角三角形30度角性质,锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
【题目】某校准备在国庆节期间组织学生到泰山进行研学旅行,已知老师与学生一共25人参加此次研学旅行,购买门票共花费1700元,门票费用如表格所示,求参加研学旅行的老师和学生各有多少人?设老师有x人,学生有y人,则可列方程组为( )
景点 | 票价 | 开放时间 |
泰山门票 | 旺季:125元/人 淡季:100元/人 | 全天 |
说明:(1)旺季时间(2月~11月),淡季时间(12月-次年1月); (2)老年人(60岁~70岁)、学生、儿童(1.2米~1.4米)享受5折优惠; (3)教师、省部级劳模、英模、道德模范享受8折优惠; (4)现役军人、伤残军人、70岁以上老年人、残疾人,凭本人有效证件免费进山; (5)享受优惠的游客请出示本人有效证件。 | ||
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()