题目内容
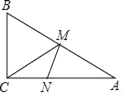
【题目】如图,在△ABC中,BC的垂直平分线交AC于点E,交BC于点D,且AD=AB,连接BE交AD于点F,下列结论:( )
①∠EBC=∠C;②△EAF∽△EBA;③BF=3EF;④∠DEF=∠DAE,其中结论正确的个数有

A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】分析: 要解答本题,首先由中垂线的性质可以求得BE=CE,利用外角与内角的关系可以得出∠CAD=∠ABE,通过作辅助线利用等腰三角形的性质和三角形全等可以得出EF=FH=![]() HB,根据等高的两三角形的面积关系求出AF=DF,利用角的关系代替证明∠5≠∠4,从而得出△DEF与△DAE不相似.根据以上的分析可以得出正确的选项答案.
HB,根据等高的两三角形的面积关系求出AF=DF,利用角的关系代替证明∠5≠∠4,从而得出△DEF与△DAE不相似.根据以上的分析可以得出正确的选项答案.
详解: ∵BC的垂直平分线交AC于点E,交BC于点D,
∴CE=BE,
∴∠EBC=∠C,故①正确;
∵AD=AB,
∴∠8=∠ABC=∠6+∠7,
∵∠8=∠C+∠4,
∴∠C+∠4=∠6+∠7,
∴∠4=∠6,
∵∠AEF=∠AEB,
∴△EAF∽△EBA,故②正确;
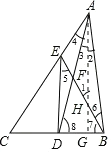
作AG⊥BD于点G,交BE于点H,
∵AD=AB,DE⊥BC,
∴∠2=∠3,DG=BG=![]() BD,DE∥AG,
BD,DE∥AG,
∴△CDE∽△CGA,△BGH∽△BDE,DE=AH,∠EDA=∠3,∠5=∠1,
∴在△DEF与△AHF中,
∠EDA=∠3
∠5=∠1
DE=AH,
∴△DEF≌△AHF(AAS),
∴AF=DF,EF=HF=![]() EH,且EH=BH,
EH,且EH=BH,
∴EF:BF=1:3,故③正确;
∵∠1=∠2+∠6,且∠4=∠6,∠2=∠3,
∴∠5=∠3+∠4,
∴∠5≠∠4,故④错误,
综上所述:正确的答案有3个,
故选:C.
点睛: 本题考查了中垂线的判定及性质,等腰三角形的性质,三角形全等的判定及性质,三角形的中位线及相似三角形的判定及性质和等积变换等知识.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案【题目】近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加.某商场从厂家购进了A,B两种型号的空气净化器,两种净化器的销售相关信息见下表:
A型销售数量(台) | B型销售数量(台) | 总利润(元) |
5 | 10 | 2 000 |
10 | 5 | 2 500 |
(1)每台A型空气净化器和B型空气净化器的销售利润分别是多少?
(2)该公司计划一次购进两种型号的空气净化器共100台,其中B型空气净化器的进货量不少于A型空气净化器的2倍,为使该公司销售完这100台空气净化器后的总利润最大,请你设计相应的进货方案;
(3)已知A型空气净化器的净化能力为300 m3/小时,B型空气净化器的净化能力为200 m3/小时.某长方体室内活动场地的总面积为200 m2,室内墙高3 m.该场地负责人计划购买5台空气净化器每天花费30分钟将室内空气净化一新,如不考虑空气对流等因素,至少要购买A型空气净化器多少台?