��Ŀ����
��ͼ����֪������ ����A����3��0����B��1��0�����㣬��y�ύ�ڵ�C���䶥��ΪD���Գ�����ֱ��l��l��x�ύ�ڵ�H��
����A����3��0����B��1��0�����㣬��y�ύ�ڵ�C���䶥��ΪD���Գ�����ֱ��l��l��x�ύ�ڵ�H��
��1����������ߵĽ���ʽ��
��2������P�Ǹ������߶Գ���l�ϵ�һ�����㣬���PBC�ܳ�����Сֵ��
��3����E���߶�AD�ϵ�һ�����㣨 E��A��D���غϣ�����E����ƽ����y���ֱ�߽��������ڵ�F����x���ڵ�G�����E�ĺ�����Ϊm����ADF�����ΪS��
����S��m�ĺ�����ϵʽ��
��S�Ƿ�������ֵ�������ڣ�������ֵ����ʱ��E�����ꣻ�������ڣ���˵�����ɣ�
��1�� ����2��
����2�� +
+ ����3����
����3���� ���ڵ�m=��2ʱ��S������ֵΪ1����ʱ��E������Ϊ����2��2����
���ڵ�m=��2ʱ��S������ֵΪ1����ʱ��E������Ϊ����2��2����
���������������1����A��B��������������ߵĽ���ʽ���ɣ�
��2����B���ڶԳ���ĶԳƵ�A������AC���Գ�����P����P��������ĵ㣻��PBC���ܳ�����AC+BC��
��3�������ֱ��AD�Ľ���ʽ���ɵ�E�ĺ�����Ϊm�����Ա�ʾ����E�������ꣻ����F�ĺ�����Ҳ��m����F���������ϣ����Կ�����m��ʾ��F�������꣬��S��ADF =S��DEF+S��AEF�������S����m�ı���ʽ��
�ڰѢ��еĺ�������ʽ��Ϊ����ʽ������������ֵ�͵�E�����꣮
�����������1���������֪�� ����ã�
����ã� ���������ߵĽ���ʽΪ��
���������ߵĽ���ʽΪ�� ��
��
��2���� ����C��0��3�����ߡ�PBC���ܳ�Ϊ��PB+PC+BC��BC�Ƕ�ֵ���൱PB+PC��Сʱ����PBC���ܳ���С������ͼ1����A����B���ڶԳ���l�Գƣ�������AC��l�ڵ�P������PΪ����ĵ㣮��AP=BP�����PBC���ܳ���Сֵ�ǣ�PB+PC+BC=AC+BC����A����3��0����B��1��0����C��0��3������AC=
����C��0��3�����ߡ�PBC���ܳ�Ϊ��PB+PC+BC��BC�Ƕ�ֵ���൱PB+PC��Сʱ����PBC���ܳ���С������ͼ1����A����B���ڶԳ���l�Գƣ�������AC��l�ڵ�P������PΪ����ĵ㣮��AP=BP�����PBC���ܳ���Сֵ�ǣ�PB+PC+BC=AC+BC����A����3��0����B��1��0����C��0��3������AC= ��BC=
��BC= �����PBC���ܳ���Сֵ=
�����PBC���ܳ���Сֵ= +
+ ��
��
��3����ͼ2���١������� ����D������Ϊ����1��4����A����3��0������ֱ��AD�Ľ���ʽΪ
����D������Ϊ����1��4����A����3��0������ֱ��AD�Ľ���ʽΪ ���ߵ�E�ĺ�����Ϊm����E��m��2m+6����F��m��
���ߵ�E�ĺ�����Ϊm����E��m��2m+6����F��m�� ����
����
��EF= =
= ��
��
��S=S��DEF+S��AEF= EF•GH+
EF•GH+ EF•AG=
EF•AG= EF•AH=
EF•AH= =
= ��
��
�� =
= ���൱m=��2ʱ��S������ֵΪ1����ʱ��E������Ϊ����2��2����
���൱m=��2ʱ��S������ֵΪ1����ʱ��E������Ϊ����2��2����
���㣺���κ����ۺ��⣮

ij��Ʒ�Ľ���Ϊÿǧ��40Ԫ�����۵��������������Ĺ�ϵ���±���ÿǧ���ۼ۲��ܸ���65Ԫ����
| ���۵���(Ԫ) | 50 | 53 | 56 | 59 | 62 | 65 |
| ����������ǧ�ˣ� | 420 | 360 | 300 | 240 | 180 | 120 |
��1����y��x�ĺ�����ϵʽ����ֱ��д���Ա���x��ȡֵ��Χ��
��2��ÿǧ����Ʒ���ۼ۶�Ϊ����Ԫʱ��ÿ���¿ɻ��������������������Ƕ���Ԫ��
ij��������ijƷ�ƵĻ��۵ƣ��������۵ư������ֳ�15���ȼ����ȼ�Խ�ߣ�����Խ�ã��磺������Ʒ����һ����Ʒ�����������������۵ƣ�һ����Ʒÿ̨�ɻ���21Ԫ��ÿ���һ���ȼ�ÿ̨�ɶ������1Ԫ������ÿ��ֻ������ͬһ���ȼ��Ļ��۵ƣ�ÿ���ȼ�ÿ��������̨�����±���ʾ��
| �ȼ���x���� | һ�� | ���� | ���� | �� |
| ��������y̨/�죩 | 78 | 76 | 74 | �� |
��2��ÿ̨���۵ƿɻ���z��Ԫ�����ڵȼ�x�������ĺ�����ϵʽ��______��
��3���������������������Ļ��۵�ȫ���۳�������Ӧ������һ�ȼ��Ļ��۵ƣ����ܻ�����������������Ƕ��٣�
 .
. ������0,-1��,��3,2�����㣮�����Ľ���ʽ���������꣮
������0,-1��,��3,2�����㣮�����Ľ���ʽ���������꣮
 ��ȡֵ��Χ��
��ȡֵ��Χ�� ��ͬһֱ��
��ͬһֱ�� �ϣ��ҵ�
�ϣ��ҵ� ���
��� �غϡ��̶ֹ�
�غϡ��̶ֹ� ����
���� ��ÿ��1����λ���ȵ��ٶ���
��ÿ��1����λ���ȵ��ٶ��� ���
��� �غ�ʱ�˶�ֹͣ����ƽ��ʱ��Ϊ
�غ�ʱ�˶�ֹͣ����ƽ��ʱ��Ϊ �롣
�롣
 ��ǡ�þ�����
��ǡ�þ����� ����
���� ����ֱ��д��
����ֱ��д�� Ϊ�߶�
Ϊ�߶� ��һ�㣬��һ����
��һ�㣬��һ����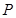 �ӵ�
�ӵ� �����˶��������
�����˶�������� �����˶������
�����˶������
 ��
�� �ύ�ڵ�A(��1��0)��B(3��0)����
�ύ�ڵ�A(��1��0)��B(3��0)���� �ύ�ڵ�C(0��3)��
�ύ�ڵ�C(0��3)��
 ����ƽ��
����ƽ��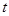
 ����λ���ȣ�ʹ֮����
����λ���ȣ�ʹ֮���� ����
����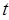 ��ֵ��
��ֵ��