题目内容
如图,黎叔叔想用60m长的篱笆靠墙MN围成一个矩形花圃ABCD,已知墙长MN=30m.
(1)能否使矩形花圃ABCD的面积为400m2?若能,请说明围法;若不能,请说明理由.
(2)请你帮助黎叔叔设计一种围法,使矩形花圃ABCD的面积最大,并求出最大面积.
(1)能,长为20m,宽为20m;(2)长为30m,宽为15m时,面积最大为:450.
解析试题分析:(1)由于篱笆总长为30m,设垂直于墙的AB边长为 m,由此得到BD=(
m,由此得到BD=(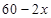 )m,接着根据题意列出方程
)m,接着根据题意列出方程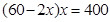 ,解方程即可求出AB的长;
,解方程即可求出AB的长;
(2)根据(1)得到矩形花圃ABCD的面积为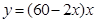 ,求出此函数的最值即可.
,求出此函数的最值即可.
试题解析:(1)依题意可知:AB边长为 m,由此得到BD=(
m,由此得到BD=(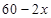 )m,∴
)m,∴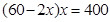 ,解得:
,解得: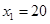 ,
,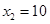 .当
.当 时,BD=
时,BD=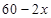 =20,当
=20,当 时,BD=
时,BD=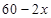 =40>30,∵墙可利用的最大长度为15m,∴
=40>30,∵墙可利用的最大长度为15m,∴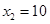 舍去.∴AB的长为20m,BD的长为20m;
舍去.∴AB的长为20m,BD的长为20m;
(2)设AB边长为 m,花圃的面积为
m,花圃的面积为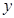 ,则
,则 .
.
∴当 时,
时, .而当
.而当 时,BD=
时,BD=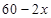 =30,可以构成矩形.
=30,可以构成矩形.
∴当 时,BD=
时,BD=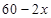 =30,可以构成的矩形的面积最大,为450
=30,可以构成的矩形的面积最大,为450 .
.
考点:1.一元二次方程的应用;2.二次函数的性质.

练习册系列答案
相关题目
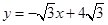 与x轴相交于点A,与直线
与x轴相交于点A,与直线 相交于点P.动点E从原点O出发,以每秒1个单位长度的速度沿着OPA的路线向点A匀速运动(E不与点O,A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分面积为S.
相交于点P.动点E从原点O出发,以每秒1个单位长度的速度沿着OPA的路线向点A匀速运动(E不与点O,A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分面积为S.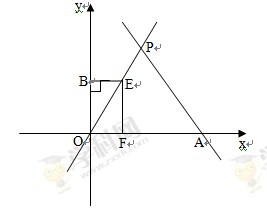

 ,抛物线
,抛物线 过A、B两点.
过A、B两点.
 在同一直线
在同一直线 上,且点
上,且点 与点
与点 重合。现固定
重合。现固定 ,将
,将 以每秒1个单位长度的速度在
以每秒1个单位长度的速度在 与点
与点 重合时运动停止。设平移时间为
重合时运动停止。设平移时间为 秒。
秒。
 边恰好经过点
边恰好经过点 ;当
;当 ,请直接写出
,请直接写出 为线段
为线段 上一点,若一动点
上一点,若一动点 从点
从点 方向运动,到达点
方向运动,到达点 方向运动到达点
方向运动到达点




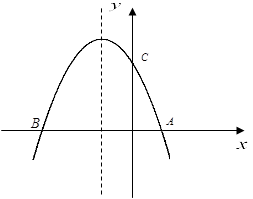
 与x轴交与点A(1,0)与点B, 且过点C(0,3),
与x轴交与点A(1,0)与点B, 且过点C(0,3),