题目内容
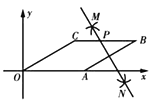
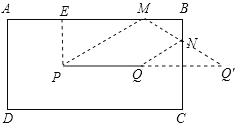
【题目】如图,长方形台球桌面ABCD上有两个球P,Q.PQ∥AB,球P连续撞击台球桌边AB,BC反射后,撞到球Q.已知点M,N是球在AB,BC边的撞击点,PQ=4,∠MPQ=30,且点P到AB边的距离为3,则四边形PMNQ的周长为__.

【答案】16.
【解析】
作PE⊥AB于E,则PE=3,延长PQ、MN交于点Q',证出Q与Q'关于BC对称,MP=2PE=6,由轴对称的性质得出NQ'=NQ,证出∠Q'=30°=∠MPQ,得出MQ'=MP=6,即可得出答案.
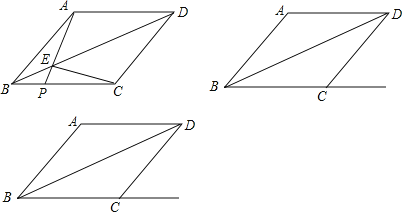
作PE⊥AB于E,则PE=3,延长PQ、MN交于点Q',如图所示:
∵四边形ABCD是矩形,
∴∠B=90°,AB⊥BC.
∵PQ∥AB,
∴PQ⊥BC,∠EMP=∠MPQ=30°,∠Q'=∠BMN,
∴Q与Q'关于BC对称,MP=2PE=6,
∴NQ'=NQ,
由题意得:∠BMN=∠EMP=30°,
∴∠Q'=30°=∠MPQ,
∴MQ'=MP=6,
∴四边形PMNQ的周长=MP+PQ+NQ+MN=MP+PQ+NQ'+MN=MP+PQ+MQ'=6+4+6=16.
故答案为:16.

练习册系列答案
相关题目