题目内容
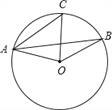
【题目】(1)如图,在⊙O中,AC∥OB,∠BAO=25°,求∠BOC的度数.
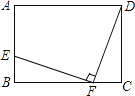
(2)已知:如图,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF,求证:BF=CD.
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:(1)本题利用半径相等和平行线的性质,圆周角定理得出结论即可;(2)本题利用等角的余角相等得出角相等,得出三角形全等即可.
试题解析:
(1)∵OA=OB,
∴∠B=∠BAO=25°,
∵AC∥OB,
∴∠BAC=∠B=25°,
∴∠BOC=2∠BAC=50°.
(2)∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∵EF⊥DF,
∴∠EFD=90°,
∴∠EFB+∠CFD=90°,
∵∠EFB+∠BEF=90°,
∴∠BEF=∠CFD,
在△BEF和△CFD中,
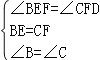 ,
,
∴△BEF≌△CFD(ASA),
∴BF=CD.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
