题目内容
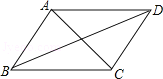
【题目】如图，在平面直角坐标系中，OA⊥OB，AB⊥x轴于点C，点A（
，1）在反比例函数
的图象上．
（1）求反比例函数的表达式；
（2）在x轴的负半轴上存在一点P，使得S△AOP=
S△AOB，求点P的坐标；
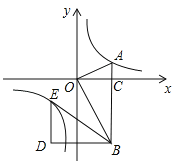
（3）若将△BOA绕点B按逆时针方向旋转60°得到△BDE．直接写出点E的坐标，并判断点E是否在该反比例函数的图象上，说明理由．
【答案】（1）
；（2）P（
，0）；（3）E（
，﹣1），在．
【解析】
试题分析：（1）将点A（
，1）代入
，利用待定系数法即可求出反比例函数的表达式；
（2）先由射影定理求出BC=3，那么B（，﹣3），计算求出S△AOB=
××4=
．则S△AOP=S△AOB=．设点P的坐标为（m，0），列出方程求解即可；
（3）先解△OAB，得出∠ABO=30°，再根据旋转的性质求出E点坐标为（﹣，﹣1），即可求解．
试题解析：（1）∵点A（，1）在反比例函数的图象上，∴k=×1=，∴反比例函数的表达式为；
（2）∵A（，1），AB⊥x轴于点C，∴OC=，AC=1，由射影定理得
=ACBC，可得BC=3，B（，﹣3），S△AOB=××4=，∴S△AOP=S△AOB=
．
设点P的坐标为（m，0），∴×|m|×1=，∴|m|=，∵P是x轴的负半轴上的点，∴m=﹣，∴点P的坐标为（，0）；
（3）点E在该反比例函数的图象上，理由如下：
∵OA⊥OB，OA=2，OB=，AB=4，∴sin∠ABO=
=
=，∴∠ABO=30°，∵将△BOA绕点B按逆时针方向旋转60°得到△BDE，∴△BOA≌△BDE，∠OBD=60°，∴BO=BD=，OA=DE=2，∠BOA=∠BDE=90°，∠ABD=30°+60°=90°，而BD﹣OC=
，BC﹣DE=1，∴E（，﹣1），∵×（﹣1）=
，∴点E在该反比例函数的图象上．
