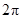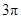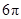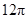题目内容
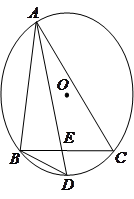
如图,在△ABC的外接圆O中,D是弧BC的中点,AD交BC于点E,连结BD.请考虑: BD2=DE·DA是否成立?若成立,给出证明;若不成立,举例说明.
 |
成立
连接DC,
∵∠DCB和∠DAB为同弧所对圆周角,
∴∠DCB=∠DAB.
∵∠BAD和∠CAD为等弧所对圆周角,
∴∠BAD=∠CAD.
∴∠DCE=∠DAC.
∵∠CDE=∠ADC,
∴△DEC∽△DCA.
∴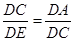
∴DC2=DE•DA.即BD2=DE·DA
∵∠DCB和∠DAB为同弧所对圆周角,
∴∠DCB=∠DAB.
∵∠BAD和∠CAD为等弧所对圆周角,
∴∠BAD=∠CAD.
∴∠DCE=∠DAC.
∵∠CDE=∠ADC,
∴△DEC∽△DCA.
∴
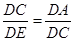
∴DC2=DE•DA.即BD2=DE·DA

练习册系列答案
相关题目
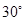 ,则∠A的度数为 ▲ .
,则∠A的度数为 ▲ .
 是正方形
是正方形 的外接圆,点
的外接圆,点 是
是 上任意一点,则∠
上任意一点,则∠ 的度数为( ▲ )
的度数为( ▲ )





 ,
, .
.
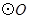 的半径
的半径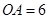 ,
,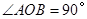 ,则
,则 所对的弧
所对的弧 的长为( )
的长为( )