题目内容
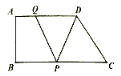
【题目】如图,![]() 中,
中,![]() 是角平分线,
是角平分线,![]() 交A
交A![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)试判断四边形![]() 的形状;
的形状;
(2)当![]() 满足______条件时,
满足______条件时,![]() ;当
;当![]() 满足_____条件时,
满足_____条件时,![]() .
.

【答案】(1)见解析;(2)AB=AC;∠BAC=90°.
【解析】
(1)根据DE∥AC交AB于点E,DF∥AB交AC于点F,可以判断四边形AEDF是平行四边形,再根据角平分线的性质和平行线的性质即可证明结论成立;
(2)因为菱形的对角线互相垂直,所以当AD⊥BC时,可得![]() ,而
,而![]() 中,
中,![]() 是角平分线,所以当AB=AC时,根据三线合一可得AD⊥BC;根据正方形的对角线相等,而有一个角是直角的菱形是正方形即可解答
是角平分线,所以当AB=AC时,根据三线合一可得AD⊥BC;根据正方形的对角线相等,而有一个角是直角的菱形是正方形即可解答
(1)四边形AEDF是菱形
∵DE∥AC,DF∥AB
∴四边形AEDF是平行四边形,
∠FAD=∠EDA,
又∠FAD=∠EAD,
∴∠EDA=∠EAD,
∴ED=EA,
∴四边形AEDF是菱形
(2)当![]() 满足AB=AC 条件时,
满足AB=AC 条件时,![]() ,
,
理由:∵四边形AEDF是菱形
∴AD⊥EF,
当AB=AC时,∵![]() 是角平分线,
是角平分线,
∴AD⊥BC,
∴![]() ;
;
当![]() 满足∠BAC=90°条件时,
满足∠BAC=90°条件时,![]() .
.
理由:∵四边形AEDF是菱形,∠BAC=90°
∴菱形AEDF是正方形,
∴![]() .
.

练习册系列答案
相关题目