Question

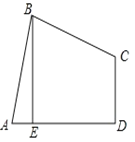
【题目】如图所示，在直角梯形中，，，，，．动点从点出发，沿边向点以每秒2个单位长的速度运动，动点同时从点出发，在边上以每秒1个单位长的速度向点运动，当其中一个动点到达端点时另一个动点也随之停止运动．设运动的时间为（秒），

（1）①设的面积为，求与之间的函数关系式，并写出自变量的取值范围；

②当为何值时，？能不能等于？为什么？

（2）①当为何值时，？

②当为何值时，点是在的垂直平分线上？

Answer 1

【答案】（1）①S=﹣2t+12(0＜t≤4.5）；②S不能等于2；（2）①当t=3时，四边形PCDQ是平行四边形．②当t=时，点Q是在PD的垂直平分线上.

【解析】

（1）①过点P作PE⊥AD于E，可得四边形ABPE是矩形，PE=AB=4，又因为DQ=6﹣t，可得与之间的函数关系式，根据，点从点出发，沿边向点以每秒2个单位长的速度运动，可得x取值范围；②设s=6,s=2即可解答；（2）①当PQ∥CD时，又因为 DQ∥CP，所以四边形PCDQ是平行四边形，可得PC=DQ，从而求解；②A因为E=BP=2t，PE=AB=4，QE=AE-AQ=BP-AQ=2t﹣t=t，所以当点Q是在PD的垂直平分线上时，DQ=PQ，DQ2=PQ2，根据勾股定理得t2+42=（6﹣t）2，从而求解.

（1）①直角梯形ABCD中，AD∥BC，∠A=90°，BC=9，AB=4，AD=6，

依题意AQ=t，BP=2t，则DQ=6﹣t，CP=9﹣2t，

过点P作PE⊥AD于E，

则四边形ABPE是矩形，PE=AB=4，

∴S=DQAB=（6﹣t）×4=﹣2t+12(0＜t≤4.5）．

②当S=6时，﹣2t+12=6，

解得，t=3，

∴当t=3时，S=6，

当S=2时，﹣2t+12=2，

解得，t=5＞4.5

∴S不能等于2；

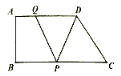
（2）①当PQ∥CD时，∵DQ∥CP，

∴四边形PCDQ是平行四边形，∴PC=DQ，

∴9﹣2t=6﹣t解得：t=3，

∴当t=3时，四边形PCDQ是平行四边形．

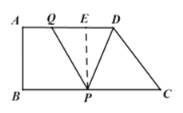
②AE=BP=2t，PE=AB=4，

QE=AE-AQ=BP-AQ=2t﹣t=t，

当点Q是在PD的垂直平分线上时，DQ=PQ，DQ2=PQ2，

∴t2+42=（6﹣t）2，

解得：t=

∴当t=时，点Q是在PD的垂直平分线上.