题目内容
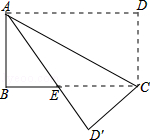
【题目】如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE. 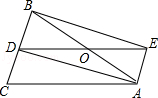
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
【答案】
(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形,
∵AB=AC,AD是∠BAC的角平分线,
∴AD⊥BC,
∴∠ADB=90°,
∴平行四边形AEBD是矩形;
(2)当∠BAC=90°时,
理由:∵∠BAC=90°,AB=AC,AD是∠BAC的角平分线,
∴AD=BD=CD,
∵由(1)得四边形AEBD是矩形,
∴矩形AEBD是正方形.
【解析】(1)利用平行四边形的判定首先得出四边形AEBD是平行四边形,进而由等腰三角形的性质得出∠ADB=90°,即可得出答案;(2)利用等腰直角三角形的性质得出AD=BD=CD,进而利用正方形的判定得出即可.
【考点精析】根据题目的已知条件,利用矩形的判定方法和正方形的判定方法的相关知识可以得到问题的答案,需要掌握有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形;先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目