Question

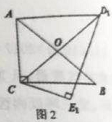
【题目】如图，在矩形ABCD中，E是AB边的中点，F在AD边上，M，N分别是CD，BC边上的动点，若AB=AF=2，AD=3，则四边形EFMN周长的最小值是（ ）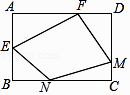
A.2+
B.2 +2
C.5+
D.8

Answer 1

【答案】C
【解析】解：如图所示，延长EB至G，使BE=BG，延长FD到H，使DF=DH，连接GN，MH，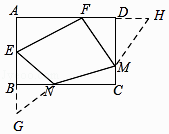
∴BC垂直平分EG，CD垂直平分FH，
∴EN=GN，MF=MH，
∵E是AB边的中点，F在AD边上，AB=AF=2，AD=3，
∴EF长不变，AE=EB=BG=1，DF=DH=1，
即AG=3，AH=4，
∵M，N分别是CD，BC边上的动点，
∴当点G、N、M、H在同一直线上时，GN+MN+MH=GH最短，
即EN+MN+MF最短，
此时Rt△AGH中，GH= = =5，
∴EN+MN+MF=5，
又∵Rt△AEF中，EF= = ，
∴EN+MN+MF+EF=5+ ，
∴四边形EFMN周长的最小值是5+ ，
故选：C．
【考点精析】利用矩形的性质对题目进行判断即可得到答案，需要熟知矩形的四个角都是直角，矩形的对角线相等．