题目内容
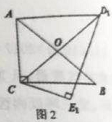
【题目】把一副三角板如图(1)放置,其中∠ACB=∠DEC=90°,斜边AB=6,DC=7,把三角板DCE绕着点C顺时针旋转使CD边恰好过AB的中点O,得到△D1CE1如图(2),则线段AD1的长度为( )

A. 3![]() B. 5 C. 4 D.
B. 5 C. 4 D. ![]()
【答案】B
【解析】分析: 先求出∠ACD=30°,再根据旋转角求出∠ACD1=45°,然后判断出△ACO是等腰直角三角形,再根据等腰直角三角形的性质求出AO,CO,AB⊥CO,再求出OD1然后利用勾股定理列式计算即可得解.
详解: ∵∠ACB=∠DEC=90°,∠D=30°,
∴∠DCE=90°-30°=60°,
∴∠ACD=90°-60°=30°,
∵旋转角为15°,
∴∠ACD1=30°+15°=45°,
又∵∠A=45°,
∴△ACO是等腰直角三角形,
∴AO=CO=![]() AB=
AB=![]() ,AB⊥CO,
,AB⊥CO,
∵DC=7,
∴D1C=DC=7,
∴D1O=7-3=4,
在Rt△AOD1中,AD1=![]() ,
,
故选B.

练习册系列答案
相关题目