Question

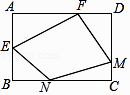
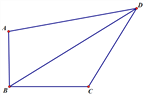
【题目】如图，在四边形ABCD 中，∠ABC＝90°，AB＝6，BC＝8，CD＝10，AD＝10 ，

(1)求四边形ABCD的面积(2)求 BD的长

Answer 1

【答案】（1）74；（2）2

【解析】（1）根据勾股定理的逆定理得出△ABC是直角三角形，进而求出四边形面积即可；

（2）过点D作DE⊥BC，交BC的延长线与点E,利用△ABC∽△CED求出BD的长即可．

（1）连接AC,

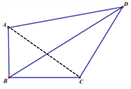
∵∠ABC=90°,

∴△ABC为直角三角形,AB=8,BC=6，∴AC=10，

又∵DA=10，CD=10，

∴102+102=（10）2

AC2+CD2=DA2

所以△ACD为直角三角形.

四边形ABCD的面积S△ABC+S△ACD==74;

(2) 过点D作DE⊥BC，交BC的延长线与点E

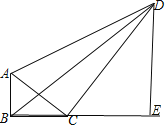
∵∠DEC=90°,∴∠DCE+∠CDE=90°，

所以∠DCE+∠ACB=90°，

∴∠CDE=∠ACB,又∵∠ABC=90°，

∴△ABC∽△CED

∴

∴CE=6，DE=8.

∴BE=BC+CE=14，

在Rt△DEB中，

DB=.