题目内容
【题目】如图，射线OP过Rt△ABC的边AC、AB的中点M、N，AC=4cm，BC=4 
cm，OM=3cm．射线OP上有一动点Q从点O出发，沿射线OP以每秒1cm的速度向右移动，以Q为圆心，QM为半径的圆，经过t秒与BC、AB中的一边所在的直线相切，请写出t的所有可能值（单位：秒） 
【答案】1s或5s或（4+ 
）s
【解析】解：如图，作OG⊥AB于G，由题意OG= 
ON= 
＞3，所以⊙Q在AC的左边不可能与AB相切．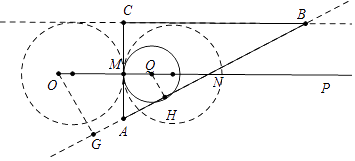 
相切有三种可能：当⊙Q与BC相切时，MQ=2，
∴|t﹣3|=2，
∴t=1或5．
当⊙Q与AB相切时，设切点为H，连接QH．
易知QN=2QH，
∴2+2 =2（t﹣3），
解得t=4+ ，
综上所述，t=1s或5s或（4+ ）s时，⊙Q与BC/AB相切．
所以答案是1s或5s或（4+ ）s
【考点精析】本题主要考查了勾股定理的概念和切线的性质定理的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题．
练习册系列答案
相关题目
