题目内容
【题目】如图,菱形ABCD的边长为6,M、N分别是边BC、CD上的点,且MC=2MB,ND=2NC,点P是对角线BD上一点,则PM+PN的最小值是 . 
【答案】6
【解析】解:作M关于BD的对称点M′交AB于M′,连接M′N交BD于P, 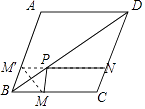
则M′N=PM+PN的最小值,
∵MC=2MB,ND=2NC,
∴BM=CN=2,
∴BM′=2,
∴BM′=CN,
∵BM′∥CN,
∴四边形BCNM′是平行四边形,
∴M′N=BC=6,
∴PM+PN的最小值=6,
所以答案是:6.
【考点精析】解答此题的关键在于理解菱形的性质的相关知识,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.

练习册系列答案
相关题目