Question

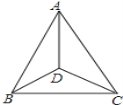
【题目】如图，在△ABC中，以AB为直径作⊙O交BC于点D，∠DAC=∠B．

（1）求证：AC是⊙O的切线；

（2）点E是AB上一点，若∠BCE=∠B，tan∠B=，⊙O的半径是4，求EC的长．

Answer 1

【答案】（1）证明见解析；（2）CE=5．

【解析】（1）欲证明AC是切线，只要证明AB⊥AC即可；

（2）设EC=EB=x，在Rt△AEC中，利用勾股定理构建方程即可解决问题.

（1）∵AB是直径，

∴∠ADB=90°，

∴∠B+∠BAD=90°，

∵∠DAC=∠B，

∴∠DAC+∠BAD=90°，

∴∠BAC=90°，

∴BA⊥AC，

∴AC是⊙O的切线．

（2）∵∠BCE=∠B，

∴EC=EB，设EC=EB=x，

在Rt△ABC中，tan∠B=，AB=8，

∴AC=4，

在Rt△AEC中，∵EC2=AE2+AC2，

∴x2=（8﹣x）2+42，

解得x=5，

∴CE=5．