题目内容
被誉为东昌三宝之首的铁塔,始建于北宋时期,是我市现存的最古老的建筑。如图,已知测角仪AC高为1.6米,CD的长为6米,在C点测的塔顶E的仰角为45°,在D点测的塔顶E的仰角为60°,CD所在的水平线CG⊥EF于G,求铁塔EF的高。(结果精确到0.1米)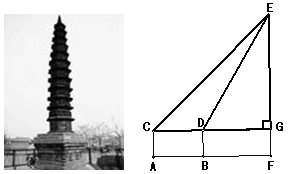

15.8米
解:设EG=x米
在RT△CEG中,∵∠ECG=45°,∴∠CEG=45°,
∴∠ECG=∠CEG,∴CG=EG=x米。
在RT△DEG中,∠EDG=60°,tan∠EDG=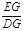 ,
,
∴DG=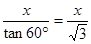
∵CG-DG="CD=6," ∴x-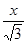 =6,
=6,
解得x=9+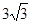
∴EF=EG+GF=9+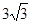 +1.6≈15.8
+1.6≈15.8
所以铁塔的高约为15.8米
根据已知得出EG=CG,进而求出CD+DG=EG,再利用测角仪AC的高为1.6m,求出铁塔EF的高即可.
在RT△CEG中,∵∠ECG=45°,∴∠CEG=45°,
∴∠ECG=∠CEG,∴CG=EG=x米。
在RT△DEG中,∠EDG=60°,tan∠EDG=
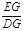 ,
,∴DG=
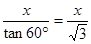
∵CG-DG="CD=6," ∴x-
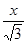 =6,
=6,解得x=9+
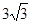
∴EF=EG+GF=9+
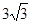 +1.6≈15.8
+1.6≈15.8所以铁塔的高约为15.8米
根据已知得出EG=CG,进而求出CD+DG=EG,再利用测角仪AC的高为1.6m,求出铁塔EF的高即可.

练习册系列答案
相关题目
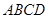 中,以点
中,以点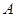 为圆心,
为圆心,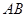 为半径的圆,交
为半径的圆,交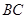 于点
于点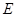 .
.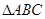 ≌
≌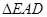 ;
;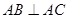 ,
,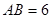 ,
,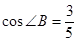 ,求
,求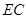 的长.
的长.
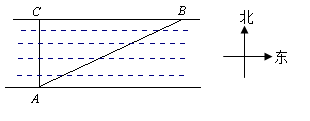
 的坡比
的坡比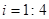 ,如果坡高
,如果坡高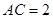 米,那么它的水平宽度
米,那么它的水平宽度 的长是
的长是  米.
米.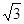 tan(a+10°)=1,则锐角a的读数为( )
tan(a+10°)=1,则锐角a的读数为( )