题目内容
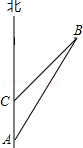
如图，一轮船在O处测得小岛A在北偏西60°的方向上，则∠AOB=30°轮船继续往正西航行100海里到达B处，测得此时∠OBA=135°，如果轮船继续往西航行，那么小岛A离轮船的最近距离是多少海里?（答案保留根号）（8分）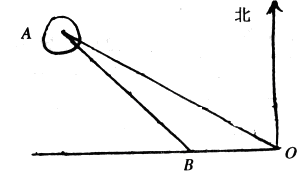
过A点作OB的垂线AC，垂足为C.则AC的长就是小岛离轮船的最近距离
∵∠OBA=135°，∴∠ABC=45°，∴△ABC是等腰直角三角形
设AC=x，则BC="x"
在Rt△AOC中，∵∠AOC=30°，AC=x，∴AO=2x，∵OB=100，OC=OB+BC，∴OC=100+x.
在Rt△AOC中，由勾股定理得（2x）2=x2+（100+x）2.
解得x1=50+50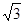
， x2=50-50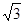（舍去）
答：小岛离轮船的最近距离是50+50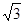海里
∵∠OBA=135°，∴∠ABC=45°，∴△ABC是等腰直角三角形
设AC=x，则BC="x"
在Rt△AOC中，∵∠AOC=30°，AC=x，∴AO=2x，∵OB=100，OC=OB+BC，∴OC=100+x.
在Rt△AOC中，由勾股定理得（2x）2=x2+（100+x）2.
解得x1=50+50
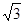， x2=50-50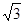（舍去）答：小岛离轮船的最近距离是50+50
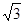海里过点A作AC⊥OB，根据三角函数关系，用BC表示出AC，再由BO=100可得出AC的长度，也即最短距离．
练习册系列答案
相关题目
）
_______________．
．
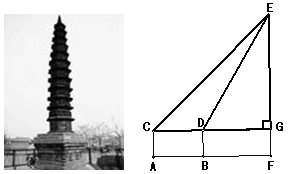
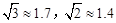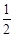
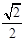
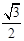
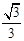
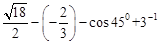