题目内容

21、如图甲，在△ABC中，E是AC边上的一点，
（1）在图甲中，作出以BE为对角线的平行四边形BDEF，使D、F分别在BC和AB边上；
（2）改变点E的位置，则图甲中所作的平行四边形BDEF有没有可能为菱形？若有，请在图乙中作出点E的位置（用尺规作图，并保留作图痕迹）；若没有，请说明理由．
分析：根据菱形的判定和平行四边形的性质作图．
解答：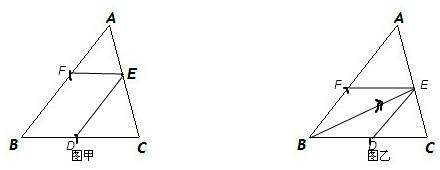
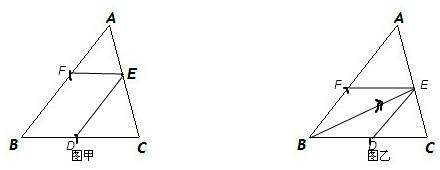
解：（1）过点E分别作ED∥AB交BC于点D，EF∥BC交AB于点F，四边形BDEF即为所求．
（2）先作∠ABC的平分线BE交AC于点E，
再过点E分别作ED∥AB交BC于点D，EF∥BC交AB于点F，
四边形BDEF即为所求．
点评：本题考查了尺规作图，要掌握菱形的判别方法是说明一个四边形为菱形的理论依据，常用三种方法：
①定义；
②四边相等；
③对角线互相垂直平分．具体选择哪种方法需要根据已知条件来确定．
练习册系列答案
相关题目
如图甲，在△ABC中，∠ACB为锐角，点D为射线BC上一点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．
解答下列问题：
（1）如果AB=AC，∠BAC=90°，
①当点D在线段BC上时（与点B不重合），如图乙，线段CF，BD之间的位置关系为
 
，数量关系为
 
．
②当点D在线段BC的延长线时，如图丙，①中的结论是否仍然成立，为什么？
（2）如果AB≠AC，∠BAC≠90°，点D在线段BC上运动．
试探究：当△ABC满足一个什么条件时，CF⊥BC（点C，F重合除外）画出相应图形，并说明理由．（画图不写作法）
（3）若AC=4
2
，BC=3，在（2）的条件下，设正方形ADEF的边DE与线段CF相交于点P，求线段CP长的最大值．
精英家教网
27、如图甲，在△ABC中，∠ACB为锐角，点D为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．解答下列问题：
（1）如果AB=AC，∠BAC=90°，
①当点D在线段BC上时（与点B不重合），如图乙，线段CF、BD之间的位置关系为
垂直
，数量关系为
相等
．
②当点D在线段BC的延长线上时，如图丙，①中的结论是否仍然成立，为什么？
（2）如果AB≠AC，∠BAC≠90°点D在线段BC上运动．试探究：当△ABC满足一个什么条件时，CF⊥BC（点C、F重合除外）？并说明理由．
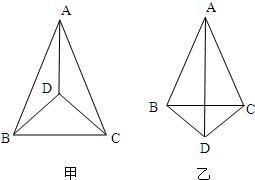24、（1）如图甲，在△ABC中，AB=AC，AD平分∠BAC，则BD与CD相等吗？请说明理由；
（2）若将图甲变为图乙，其他条件不变，则BD与CD仍相等吗？请说明理由．
如图甲，在△ABC中，AB=AC，AB的垂直平分线交AB于N，交BC的延长线于M，∠A=40°．
（1）求∠NMB的大小．
（2）如图乙，如果将（1）中∠A的度数改为70°，其余条件不变，再求∠NMB的大小．
（3）根据（1）（2）的计算，你能发现其中的蕴涵的规律吗？请写出你的猜想并证明．
（4）如图丙，将（1）中的∠A改为钝角，其余条件不变，对这个问题规律的认识是否需要加以修改？请你把∠A代入一个钝角度数验证你的结论．
如图甲，在△ABC中，∠ACB为锐角．点D为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．如果AB=AC，∠BAC=90°．
解答下列问题：
（1）当点D在线段BC上时（与点B不重合），如图甲，线段CF、BD之间的位置关系为
垂直
垂直
，数量关系为
相等
相等
．
（2）当点D在线段BC的延长线上时，如图乙，①中的结论是否仍然成立，为什么？（要求写出证明过程）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网