题目内容
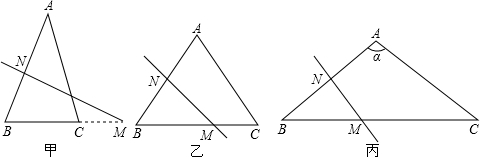
如图甲,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交BC的延长线于M,∠A=40°.
(1)求∠NMB的大小.
(2)如图乙,如果将(1)中∠A的度数改为70°,其余条件不变,再求∠NMB的大小.
(3)根据(1)(2)的计算,你能发现其中的蕴涵的规律吗?请写出你的猜想并证明.
(4)如图丙,将(1)中的∠A改为钝角,其余条件不变,对这个问题规律的认识是否需要加以修改?请你把∠A代入一个钝角度数验证你的结论.
(1)求∠NMB的大小.
(2)如图乙,如果将(1)中∠A的度数改为70°,其余条件不变,再求∠NMB的大小.
(3)根据(1)(2)的计算,你能发现其中的蕴涵的规律吗?请写出你的猜想并证明.
(4)如图丙,将(1)中的∠A改为钝角,其余条件不变,对这个问题规律的认识是否需要加以修改?请你把∠A代入一个钝角度数验证你的结论.

分析:(1)由在△ABC中,AB=AC,∠A=40°,根据等腰三角形的性质,即可求得∠B的度数,又由AB的垂直平分线交AB于N,交BC的延长线于M,即可求得∠NMB的大小.
(2)求解方法同(1);
(2)由在△ABC中,AB=AC,根据等腰三角形的性质,即可用∠A表示出∠B,又由AB的垂直平分线交AB于N,交BC的延长线于M,即可求得∠NMB与∠A的关系.
(4)解题方法同(1).
(2)求解方法同(1);
(2)由在△ABC中,AB=AC,根据等腰三角形的性质,即可用∠A表示出∠B,又由AB的垂直平分线交AB于N,交BC的延长线于M,即可求得∠NMB与∠A的关系.
(4)解题方法同(1).
解答:解:(1)∵在△ABC中,AB=AC,∠A=40°,
∴∠B=∠ACB=
=70°,
∵MN是AB的垂直平分线,
∴∠NMB=90°-∠B=20°;
(2)∵在△ABC中,AB=AC,∠A=70°,
∴∠B=∠ACB=
=55°,
∵MN是AB的垂直平分线,
∴∠NMB=90°-∠B=35°;
(3)猜想:∠NMB=
∠A.
证明:∵在△ABC中,AB=AC,
∴∠B=∠ACB=
=90°-
∠A,
∵MN是AB的垂直平分线,
∴∠NMB=90°-∠B=
∠A;
(4)不需要修改.
若∠A=100°,
∵在△ABC中,AB=AC,
∴∠B=∠ACB=
=40°,
∵MN是AB的垂直平分线,
∴∠NMB=90°-∠B=50°=
∠A.
∴∠B=∠ACB=
| 180°-∠A |
| 2 |
∵MN是AB的垂直平分线,
∴∠NMB=90°-∠B=20°;
(2)∵在△ABC中,AB=AC,∠A=70°,
∴∠B=∠ACB=
| 180°-∠A |
| 2 |
∵MN是AB的垂直平分线,
∴∠NMB=90°-∠B=35°;
(3)猜想:∠NMB=
| 1 |
| 2 |
证明:∵在△ABC中,AB=AC,
∴∠B=∠ACB=
| 180°-∠A |
| 2 |
| 1 |
| 2 |
∵MN是AB的垂直平分线,
∴∠NMB=90°-∠B=
| 1 |
| 2 |
(4)不需要修改.
若∠A=100°,
∵在△ABC中,AB=AC,
∴∠B=∠ACB=
| 180°-∠A |
| 2 |
∵MN是AB的垂直平分线,
∴∠NMB=90°-∠B=50°=
| 1 |
| 2 |
点评:此题考查了等腰三角形的性质与线段垂直平分线的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目


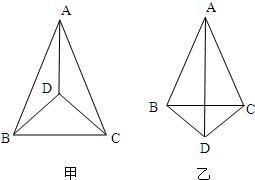 24、(1)如图甲,在△ABC中,AB=AC,AD平分∠BAC,则BD与CD相等吗?请说明理由;
24、(1)如图甲,在△ABC中,AB=AC,AD平分∠BAC,则BD与CD相等吗?请说明理由;