题目内容
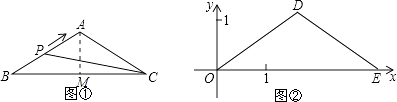
【题目】如图①，在△ABC中，AB=AC，BC=acm，∠B=30°．动点P以1cm/s的速度从点B出发，沿折线B﹣A﹣C运动到点C时停止运动．设点P出发x s时，△PBC的面积为y cm2 ． 已知y与x的函数图象如图②所示．请根据图中信息，解答下列问题：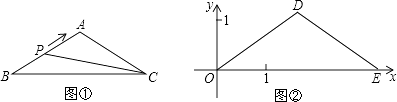 
（1）试判断△DOE的形状，并说明理由；
（2）当a为何值时，△DOE与△ABC相似？
【答案】
（1）解：△DOE是等腰三角形．
理由如下：过点A作AM⊥BC于M，
∵AB=AC，BC=acm，∠B=30°，
∴AM= 
× 
= 
a，AC=AB= a，
∴S△ABC= 
BCAM= 
a2，
∴P在边AB上时，
y= 
S△ABC= 
ax，
P在边AC上时，
y= 
S△ABC= a2﹣ ax，
作DF⊥OE于F，
∵AB=AC，点P以1cm/s的速度运动，
∴点P在边AB和AC上的运动时间相同，
∴点F是OE的中点，
∴DF是OE的垂直平分线，
∴DO=DE，
∴△DOE是等腰三角形
（2）解：由题意得：∵AB=AC，BC=acm，∠B=30°，
∴AM= × = a，
∴AB= a，
∴D（ a， a2），
∵DO=DE，AB=AC，
∴当且仅当∠DOE=∠ABC时，△DOE∽△ABC，
在Rt△DOF中，tan∠DOF= 
= 
= a，
由 a=tan30°= ，得a= 
，
∴当a= 时，△DOE∽△ABC．
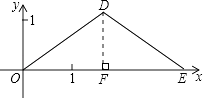
【解析】（1）首先作DF⊥OE于F，由AB=AC，点P以1cm/s的速度运动，可得点P在边AB和AC上的运动时间相同，即可得点F是OE的中点，即可证得DF是OE的垂直平分线，可得△DOE是等腰三角形；（2）设D（ a， a2），由DO=DE，AB=AC，可得当且仅当∠DOE=∠ABC时，△DOE∽△ABC，然后由三角函数的性质，即可求得当a= 时，△DOE∽△ABC．
【考点精析】关于本题考查的相似三角形的性质和解直角三角形，需要了解对应角相等，对应边成比例的两个三角形叫做相似三角形；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)才能得出正确答案．
