Question

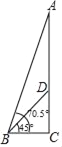
【题目】（1）如图，点，分别是锐角两边上的点，，分别以点，为圆心，以的长为半径画弧，两弧相交于点，连接，．则根据作图过程判定四边形是菱形的依据是______．

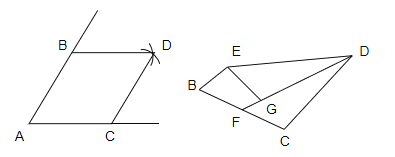
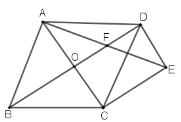
（2）如图，在菱形中，，为的中点，将沿翻折得到，射线交于点，若，则______．

Answer 1

【答案】四条边都相等的四边形是菱形

【解析】

（1）由AE＝AF＝ED＝DF，根据四条边都相等的四边形是菱形，即可证得：四边形AEDF是菱形．

（2）DE和CB的延长线相交于G'点，连结EF，作EH⊥DF于H点，如图，根据菱形的性质得A＝180°﹣∠B＝120°，AB＝AD＝2，AD∥BC，则∠1＝∠G，再利用折叠的性质得∠1＝∠2，DG＝DA＝2，EG＝EA＝1，∠3＝∠A＝120°，则∠4＝60°，在Rt△EHG中利用含30度的直角三角形三边的关系得到HG＝EG＝，EH＝EH＝，则在Rt△DEH中利用勾股定理可计算出DE＝，再证明∠2＝∠G'得到FG'＝FD，证明△AED≌△BEG'得到DE＝G'E，所以FE⊥DG'，然后证明Rt△DEF∽Rt△DHE，利用相似比计算出DF＝，则FG＝FD﹣DG＝，于是得到BF＝FG＝．

解：（1）根据作图过程判定四边形ABDC是菱形的依据是：四边相等的四边形是菱形，

理由如下：

∵根据题意得：AE＝AF＝ED＝DF，

∴四边形AEDF是菱形，

（2）DE和CB的延长线相交于G'点，连结EF，作EH⊥DF于H点，如图，

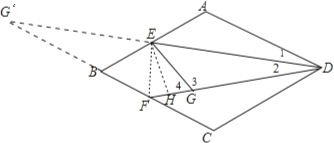
∵四边形ABCD为菱形，

∴∠A＝180°﹣∠B＝120°，AB＝AD＝2，AD∥BC

∴∠1＝∠G'，

而E为AB的中点，

∴AE＝BE＝1，

∵△AED沿DE翻折得到△GED，

∴∠1＝∠2，DG＝DA＝2，EG＝EA＝1，∠3＝∠A＝120°，

∴∠4＝60°，

∴在Rt△EHG中，HG＝EG＝，EH＝，

∴在Rt△DEH中，DE＝，

∵AD∥BG'，

∴∠1＝∠G'，

∴∠G'＝∠2，

∴FG'＝FD，

在△AED和△BEG'中，

，

∴△AED≌△BEG'，

∴DE＝G'E，AD＝BG'＝2，

∴FE⊥DG'，

∴∠FED＝90°，

∵∠HDE＝∠EDF，

∴Rt△DEF∽Rt△DHE，

∴，即，

∴DF＝，

∴FG＝FD﹣DG＝﹣2＝，

∵FG'＝FD，BG'＝DG＝2，

∴FG'－BG'＝FD－DG，

∴BF＝FG＝．

故答案为：（1）四条边都相等的四边形是菱形，（2）．